Category: R
How to get the homology of a antibody using R
What is homology?
Proteins are conserved bio molecules present in all organisms. Some proteins are conserved in many similar species, making them homologues of each other, meaning that the sequence is not the same but there is a degree of similarity.
This is measured as homology in percentage.

What is R
R is a high level programming language with a focus on statistical analysis and machine learning. R Project
R is widely used in bioinformatics and has a huge resources library of packages, most of them developed by the top Universities to help with hard to understand data, like genomic and proteomic data.
Why this matters?
This matters because antibodies will bind to specific proteins, but many proteins have similar structure and sequence. So when performing an assay you want to know what specific protein the antibody binds to.
This is also relevant when choosing an antibody that works in many species, specially when doing research in less used species, like veterinary studies.
Getting Started
You need the sequence of the epitope used to produce the antibody, I need to know where this product will bind in the target protein. If the sequence is very conserved in mammalians for example, this will be homologue in other species; eg. actins, membrane proteins, etc.
Obtaining the data
Data for sequence can be provided by the manufacturer, in some cases it will be in the terms of region of the protein, eg. 162–199aa in C-terminal of RAB22A human.
In these cases I will need to retrieve the protein sequence from UNIPROT and then cut it according to the information I have on the immunogen, this can be done using a program sequentially, like R stringi package or using an excel sheet with MID function.
Prepare environment in R (libraries)
I will use Bioconductor packages:#Install packages: rBLAST, Biostrings, annotate
install.packages("devtools")
library(devtools)
install_github("mhahsler/rBLAST")
source("https://bioconductor.org/biocLite.R")
biocLite("Biostrings")
biocLite("annotate")
These libraries will help us retrieve the homology data, and then I will use simple commands to clean and present the data in a nice way.
Cleaning data
Cleaning the data is usually 80% of the work of any data scientist.
I want the homology in simple terms of aa, or in bioinformatic terms FASTA; eg.
ATTAAGCTTATTGC
You can have terminal places, that need to be removed, usually in terms of ‘-C’, I can remove this using a simple gsub function.
dataframe$sequenceImunogen <- gsub("\\-C", "", dataframe$sequenceImunogen)
For this case the sequence is in a column called sequenceImunogen that is why I have to make a loop so the protein blast goes through all the sequences in the data frame.
The function
I will use the function blastSequences to blast the protein and obtain the homology of this specific sequence to other species. The parameters of the function can be found in the literature. I used program = “blastp” so I perform a Protein Blast, I use a hitListSize of 50 and a timeout of 200 seconds, this is from previous experience, as I will do this for multiple sequences I prefer the data to be as = data.frame.
x <- blastSequences(x = Sequence, timeout = 200, as = "data.frame", program = "blastp", hitListSize = 50)
Making a loop in R
When creating a loop in R I always put a Start variable with the Sys.time()constant, so I know how long it takes to run this loop.
Start <- Sys.time()
I have use this in a couple of hundred sequences and the result toke a few days, so keep that in mind when you run.
I first create a function that formats my results in terms of percentage of homology and give it the term percentage.
#Create a percent function
percent <- function(x, digits = 1, format = "f", ...) {
paste0(formatC(100 * x, format = format, digits = digits, ...), "%")
}
Cleaning the result data
Once the blastP results come, the 1st step is to clean unwanted information so it is not confusing, I used the base functions subset, grepl, gsub to get only information with results verified, and remove annoying characters. The objective is to have a nice table result with the best homologues.
#Remove what I do not want
x <- subset(x, grepl("_A", x$Hit_accession) == FALSE)
x <- subset(x, grepl("XP_", x$Hit_accession) == FALSE)
x <- subset(x, grepl("unnamed", x$Hit_def) == FALSE)
#Removing characters that do not
x$Species <- sub(".*\\[(.*)\\].*", "\\1", x$Hit_def, perl=TRUE)
x$Species <- gsub("/].*","", x$Species)
x$Hit_def <- gsub("[[:punct:]].*", "", x$Hit_def)
Retrieving the results above 80% identical
After I get all the results and clean a bit of the results, I want to subset the homologues to above 80%. To do this I count the total characters of the sequence using nchar function and divide the total number of hit results by this number of character, ie. for a 100 aa sequence if I hit 80 I get a 80% homology.
x$Hsp_identity <- as.numeric(x$Hsp_identity) n <- nchar(dataframe$sequenceImunogen[i]) x$percentage <- as.numeric(x$Hsp_identity/n) x<- x[order(-x$percentage), ] x<- x[x$percentage > 0.8, ] x$percentage <- percent(x$percentage)
I then clean the result to show as percentage.
Format nice output
I want this to be able to be presented in HTML, so I use HTML tags to create a visually pleasing table.
Because this is to be online I want to add hyperlinks to the results so my customers can see the result and analyse the data.
x$link <- paste0("https://www.ncbi.nlm.nih.gov/protein/",x$Hit_accession)
x$final <- paste(x$Hit_def, x$Species, x$percentage, sep = " - ")
x <- subset(x,!duplicated(x$final))
x$TOTAL <- paste0("<a href='",x$link,"'target='_blank'>",x$final,"</a>")
I Remove also any duplicated information from our table, and paste all the result into a new column, with all results separated by
(line break in HTML), to do this I use the function paste, with the option collapse = “<br>”
This will create hopefully a table like following:

All the code
All the code can be seen bellow: Use TryCatch for error management, sometimes the functions times out and you need to rerun, you get a prompt asking to skip or run again, a simple Y is enough.
Start <- Sys.time()
for (i in 1:nrow(dataframe)) {
tryCatch({
percent <- function(x, digits = 1, format = "f", ...) { paste0(formatC(100 * x, format = format, digits = digits, ...), "%")
}
x <- blastSequences(x = dataframe$sequenceImunogen[i], timeout = 200, as = "data.frame", program = "blastp", hitListSize = 50)
#Remove what I do not want
x <- subset(x, grepl("_A", x$Hit_accession) == FALSE)
x <- subset(x, grepl("XP_", x$Hit_accession) == FALSE)
x <- subset(x, grepl("unnamed", x$Hit_def) == FALSE)
#Removing characters that do not
x$Species <- sub(".\\[(.)\\].*", "\\1", x$Hit_def, perl=TRUE)
x$Species <- gsub("/].*","", x$Species)
x$Hit_def <- gsub("[[:punct:]].*", "", x$Hit_def)
x$Hsp_identity <- as.numeric(x$Hsp_identity)
n <- nchar(masterir2$sequenceImunogen[i])
x$percentage <- as.numeric(x$Hsp_identity/n)
x<- x[order(-x$percentage), ]
x<- x[x$percentage > 0.8, ]
x$percentage <- percent(x$percentage)
x$link <- paste0("https://www.ncbi.nlm.nih.gov/protein/",x$Hit_accession)
x$final <- paste(x$Hit_def, x$Species, x$percentage, sep = " - ")
x <- subset(x,!duplicated(x$final))
x$TOTAL <- paste0("<a href='",x$link,"'target='_blank'>",x$final,"</a>")
dataframe$Homology[i] <- paste(unlist(x$TOTAL), collapse ="</br>")
}, error=function(e{cat("ERROR :",conditionMessage(e), "\n")})
}
end <- Sys.time()
print(end - Start)
Conclusion
I can use R and the Bioinformatics packages in Bioconductor to retrieve the homology of known epitopes, this help us provide more valuable information to researchers.
Homology is important in the niche world of antibodies, there is a limited amount of money for validation and a limited amount of species that the antibodies can be tested on. With this simple program a homology can be check in a click of a button, instead of using
What next?
This can be incorporated into a small web application that can provide the homology for a specific selected product with a click off a button, saving time to search and blast on the NCBI website.
I am very new to the world of R and coding, so any comment is appreciated.
automl package: part 2/2 first steps how to
first steps: how to
For those who will laugh at seeing deep learning with one hidden layer and the Iris data set of 150 records, I will say: you’re perfectly right 🙂The goal at this stage is simply to take the first steps
fit a regression model manually (hard way)
Subject: predict Sepal.Length given other Iris parameters1st with gradient descent and default hyper-parameters value for learning rate (0.001) and mini batch size (32)
input
data(iris) xmat <- cbind(iris[,2:4], as.numeric(iris$Species)) ymat <- iris[,1] amlmodel <- automl_train_manual(Xref = xmat, Yref = ymat)output
(cost: mse) cost epoch10: 20.9340400047156 (cv cost: 25.205632342013) (LR: 0.001 ) cost epoch20: 20.6280923387762 (cv cost: 23.8214521197268) (LR: 0.001 ) cost epoch30: 20.3222407903838 (cv cost: 22.1899741289456) (LR: 0.001 ) cost epoch40: 20.0217966054298 (cv cost: 21.3908446693146) (LR: 0.001 ) cost epoch50: 19.7584058034009 (cv cost: 20.7170232035934) (LR: 0.001 ) dim X: ...input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c('actual', 'predict')
head(res)
outputactual predict [1,] 5.1 -2.063614 [2,] 4.9 -2.487673 [3,] 4.7 -2.471912 [4,] 4.6 -2.281035 [5,] 5.0 -1.956937 [6,] 5.4 -1.729314:-[] no pain, no gain ...
After some manual fine tuning on learning rate, mini batch size and iterations number (epochs):
input
data(iris)
xmat <- cbind(iris[,2:4], as.numeric(iris$Species))
ymat <- iris[,1]
amlmodel = automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
learningrate = 0.01,
minibatchsize = 2^2,
numiterations = 30
)
)
output(cost: mse) cost epoch10: 5.55679482839698 (cv cost: 4.87492997304325) (LR: 0.01 ) cost epoch20: 1.64996951479802 (cv cost: 1.50339773126712) (LR: 0.01 ) cost epoch30: 0.647727077375946 (cv cost: 0.60142564484723) (LR: 0.01 ) dim X: ...input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c('actual', 'predict')
head(res)
outputactual predict [1,] 5.1 4.478478 [2,] 4.9 4.215683 [3,] 4.7 4.275902 [4,] 4.6 4.313141 [5,] 5.0 4.531038 [6,] 5.4 4.742847Better result, but with human efforts!
fit a regression model automatically (easy way, Mix 1)
Same subject: predict Sepal.Length given other Iris parametersinput
data(iris)
xmat <- as.matrix(cbind(iris[,2:4], as.numeric(iris$Species)))
ymat <- iris[,1]
start.time <- Sys.time()
amlmodel <- automl_train(
Xref = xmat, Yref = ymat,
autopar = list(
psopartpopsize = 15,
numiterations = 5,
nbcores = 4
)
)
end.time <- Sys.time()
cat(paste('time ellapsed:', end.time - start.time, '\n'))
output(cost: mse) iteration 1 particle 1 weighted err: 22.05305 (train: 19.95908 cvalid: 14.72417 ) BEST MODEL KEPT iteration 1 particle 2 weighted err: 31.69094 (train: 20.55559 cvalid: 27.51518 ) iteration 1 particle 3 weighted err: 22.08092 (train: 20.52354 cvalid: 16.63009 ) iteration 1 particle 4 weighted err: 20.02091 (train: 19.18378 cvalid: 17.09095 ) BEST MODEL KEPT iteration 1 particle 5 weighted err: 28.36339 (train: 20.6763 cvalid: 25.48073 ) iteration 1 particle 6 weighted err: 28.92088 (train: 20.92546 cvalid: 25.9226 ) iteration 1 particle 7 weighted err: 21.67837 (train: 20.73866 cvalid: 18.38941 ) iteration 1 particle 8 weighted err: 29.80416 (train: 16.09191 cvalid: 24.66206 ) iteration 1 particle 9 weighted err: 22.93199 (train: 20.5561 cvalid: 14.61638 ) iteration 1 particle 10 weighted err: 21.18474 (train: 19.64622 cvalid: 15.79992 ) iteration 1 particle 11 weighted err: 23.32084 (train: 20.78257 cvalid: 14.43688 ) iteration 1 particle 12 weighted err: 22.27164 (train: 20.81055 cvalid: 17.15783 ) iteration 1 particle 13 weighted err: 2.23479 (train: 1.95683 cvalid: 1.26193 ) BEST MODEL KEPT iteration 1 particle 14 weighted err: 23.1183 (train: 20.79754 cvalid: 14.99564 ) iteration 1 particle 15 weighted err: 20.71678 (train: 19.40506 cvalid: 16.12575 ) ... iteration 4 particle 3 weighted err: 0.3469 (train: 0.32236 cvalid: 0.26104 ) iteration 4 particle 4 weighted err: 0.2448 (train: 0.07047 cvalid: 0.17943 ) iteration 4 particle 5 weighted err: 0.09674 (train: 5e-05 cvalid: 0.06048 ) BEST MODEL KEPT iteration 4 particle 6 weighted err: 0.71267 (train: 6e-05 cvalid: 0.44544 ) iteration 4 particle 7 weighted err: 0.65614 (train: 0.63381 cvalid: 0.57796 ) iteration 4 particle 8 weighted err: 0.46477 (train: 0.356 cvalid: 0.08408 ) ... time ellapsed: 2.65109273195267input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c('actual', 'predict')
head(res)
output
actual predict
[1,] 5.1 5.193862
[2,] 4.9 4.836507
[3,] 4.7 4.899531
[4,] 4.6 4.987896
[5,] 5.0 5.265334
[6,] 5.4 5.683173
It's even better, with no human efforts but machine timeUsers on Windows won't benefit from parallelization, the function uses parallel package included with R base...
fit a regression model experimentally (experimental way, Mix 2)
Same subject: predict Sepal.Length given other Iris parametersinput
data(iris)
xmat <- as.matrix(cbind(iris[,2:4], as.numeric(iris$Species)))
ymat <- iris[,1]
amlmodel <- automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
modexec = 'trainwpso',
numiterations = 30,
psopartpopsize = 50
)
)
output(cost: mse) cost epoch10: 0.113576786377019 (cv cost: 0.0967069106128153) (LR: 0 ) cost epoch20: 0.0595472259640828 (cv cost: 0.0831404427407914) (LR: 0 ) cost epoch30: 0.0494578776185938 (cv cost: 0.0538888075333611) (LR: 0 ) dim X: ...input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c('actual', 'predict')
head(res)
output
actual predict
[1,] 5.1 5.028114
[2,] 4.9 4.673366
[3,] 4.7 4.738188
[4,] 4.6 4.821392
[5,] 5.0 5.099064
[6,] 5.4 5.277315
Pretty good too, even better!But time consuming on larger datasets: where gradient descent should be preferred in this case
fit a regression model with custom cost (experimental way, Mix 2)
Same subject: predict Sepal.Length given other Iris parametersLet's try with Mean Absolute Percentage Error instead of Mean Square Error
input
data(iris)
xmat <- as.matrix(cbind(iris[,2:4], as.numeric(iris$Species)))
ymat <- iris[,1]
f <- 'J=abs((y-yhat)/y)'
f <- c(f, 'J=sum(J[!is.infinite(J)],na.rm=TRUE)')
f <- c(f, 'J=(J/length(y))')
f <- paste(f, collapse = ';')
amlmodel <- automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
modexec = 'trainwpso',
numiterations = 30,
psopartpopsize = 50,
costcustformul = f
)
)
output(cost: custom) cost epoch10: 0.901580275333795 (cv cost: 1.15936129555304) (LR: 0 ) cost epoch20: 0.890142834441629 (cv cost: 1.24167078564786) (LR: 0 ) cost epoch30: 0.886088388448652 (cv cost: 1.22756121243449) (LR: 0 ) dim X: ...input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c('actual', 'predict')
head(res)
output
actual predict
[1,] 5.1 4.693915
[2,] 4.9 4.470968
[3,] 4.7 4.482036
[4,] 4.6 4.593667
[5,] 5.0 4.738504
[6,] 5.4 4.914144
fit a classification model with softmax (Mix 2)
Subject: predict Species given other Iris parametersSoftmax is available with PSO, no derivative needed 😉
input
data(iris)
xmat = iris[,1:4]
lab2pred <- levels(iris$Species)
lghlab <- length(lab2pred)
iris$Species <- as.numeric(iris$Species)
ymat <- matrix(seq(from = 1, to = lghlab, by = 1), nrow(xmat), lghlab, byrow = TRUE)
ymat <- (ymat == as.numeric(iris$Species)) + 0
amlmodel <- automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
modexec = 'trainwpso',
layersshape = c(10, 0),
layersacttype = c('relu', 'softmax'),
layersdropoprob = c(0, 0),
numiterations = 50,
psopartpopsize = 50
)
)
output(cost: crossentropy) cost epoch10: 0.373706545886467 (cv cost: 0.36117608867856) (LR: 0 ) cost epoch20: 0.267034060152876 (cv cost: 0.163635821437066) (LR: 0 ) cost epoch30: 0.212054571476337 (cv cost: 0.112664100290429) (LR: 0 ) cost epoch40: 0.154158717402463 (cv cost: 0.102895917099299) (LR: 0 ) cost epoch50: 0.141037927317585 (cv cost: 0.0864623836595045) (LR: 0 ) dim X: ...input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c(paste('act',lab2pred, sep = '_'),
paste('pred',lab2pred, sep = '_'))
head(res)
tail(res)
output
act_setosa act_versicolor act_virginica pred_setosa pred_versicolor pred_virginica
1 1 0 0 0.9863481 0.003268881 0.010383018
2 1 0 0 0.9897295 0.003387193 0.006883349
3 1 0 0 0.9856347 0.002025946 0.012339349
4 1 0 0 0.9819881 0.004638452 0.013373451
5 1 0 0 0.9827623 0.003115452 0.014122277
6 1 0 0 0.9329747 0.031624836 0.035400439
act_setosa act_versicolor act_virginica pred_setosa pred_versicolor pred_virginica
145 0 0 1 0.02549091 2.877957e-05 0.9744803
146 0 0 1 0.08146753 2.005664e-03 0.9165268
147 0 0 1 0.05465750 1.979652e-02 0.9255460
148 0 0 1 0.06040415 1.974869e-02 0.9198472
149 0 0 1 0.02318048 4.133826e-04 0.9764061
150 0 0 1 0.03696852 5.230936e-02 0.9107221
change the model parameters (shape ...)
Same subject: predict Species given other Iris parameters1st example: with gradient descent and 2 hidden layers containing 10 nodes, with various activation functions for hidden layers
input
data(iris)
xmat = iris[,1:4]
lab2pred <- levels(iris$Species)
lghlab <- length(lab2pred)
iris$Species <- as.numeric(iris$Species)
ymat <- matrix(seq(from = 1, to = lghlab, by = 1), nrow(xmat), lghlab, byrow = TRUE)
ymat <- (ymat == as.numeric(iris$Species)) + 0
amlmodel <- automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
layersshape = c(10, 10, 0),
layersacttype = c('tanh', 'relu', ''),
layersdropoprob = c(0, 0, 0)
)
)
nb: last activation type may be left to blank (it will be set automatically)
2nd example: with gradient descent and no hidden layer (logistic regression)
input
data(iris)
xmat = iris[,1:4]
lab2pred <- levels(iris$Species)
lghlab <- length(lab2pred)
iris$Species <- as.numeric(iris$Species)
ymat <- matrix(seq(from = 1, to = lghlab, by = 1), nrow(xmat), lghlab, byrow = TRUE)
ymat <- (ymat == as.numeric(iris$Species)) + 0
amlmodel <- automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
layersshape = c(0),
layersacttype = c('sigmoid'),
layersdropoprob = c(0)
)
)
ToDo List
- transfert learning from existing frameworks
- add autotune to other parameters (layers, dropout, ...)
- CNN
- RNN
join the team !
https://github.com/aboulaboul/automl
automl package: part 1/2 why and how
Why & how automl package
- automl package provides:
- Deep Learning last tricks (those who have taken Andrew NG’s MOOC on Coursera will be in familiar territory)
- hyperparameters autotune with metaheuristic (PSO)
- experimental stuff and more to come (you’re welcome as coauthor!)
Deep Learning existing frameworks, disadvantages
Deploying and maintaining most Deep Learning frameworks means: Python…
R language is so simple to install and maintain in production environments that it is obvious to use a pure R based package for deep learning !
Neural Network – Deep Learning, disadvantages
- Disadvantages:
- 1st disadvantage: you have to test manually different combinations of parameters (number of layers, nodes, activation function, etc …) and then also tune manually hyper parameters for training (learning rate, momentum, mini batch size, etc …)
- 2nd disadvantage: only for those who are not mathematicians, calculating derivative in case of new cost or activation function, may by an issue.
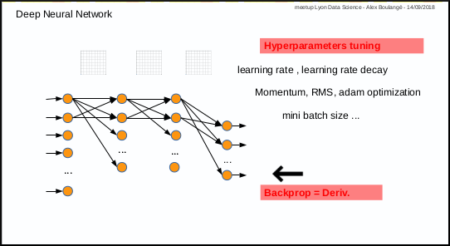
Metaheuristic – PSO, benefits
The Particle Swarm Optimization algorithm is a great and simple one.
In a few words, the first step consists in throwing randomly a set of particles in a space and the next steps consist in discovering the best solution while converging.
video tutorial from Yarpiz is a great ressource
Birth of automl package
automl package was born from the idea to use metaheuristic PSO to address the identified disadvantages above.
And last but not the least reason: use R and R only 🙂
- 3 functions are available:
- automl train manual: the manual mode to train a model
- automl train: the automatic mode to train model
- automl predict: the prediction function to apply a trained model on datas
Mix 1: hyperparameters tuning with PSO
Mix 1 consists in using PSO algorithm to optimize the hyperparameters: each particle corresponds to a set of hyperparameters.
The automl train function was made to do that.
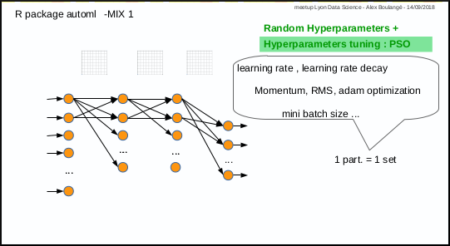
nb: parameters (nodes number, activation functions, etc…) are not automatically tuned for the moment, but why not in the futur
Mix 2: PSO instead of gradient descent
Mix 2 is experimental, it consists in using PSO algorithm to optimize the weights of Neural Network in place of gradient descent: each particle corresponds to a set of neural network weights matrices.
The automl train manual function do that too.
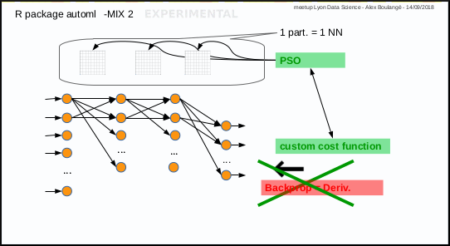
Next post
We will see how to use it in the next post.
Feel free to comment or join the team being formed
Statistics Challenge Invites Students to Tackle Opioid Crisis Using Real-World Data

In 2016, 2.1 million Americans were found to have an opioid use disorder (according to SAMHSA), with drug overdose now the leading cause of injury and death in the United States. But some of the country’s top minds are working to fight this epidemic, and statisticians are helping to lead the charge. In This is Statistics’ second annual fall data challenge, high school and undergraduate students will use statistics to analyze data and develop recommendations to help address this important public health crisis.
The contest invites teams of two to five students to put their statistical and data visualization skills to work using the Centers for Disease Control and Prevention (CDC)’s Multiple Cause of Death (Detailed Mortality) data set, and contribute to creating healthier communities. Given the size and complexity of the CDC dataset, programming languages such as R can be used to manipulate and conduct analysis effectively.
Each submission will consist of a short essay and presentation of recommendations. Winners will be awarded for best overall analysis, best visualization and best use of external data. Submissions are due November 12, 2018.
If you or a student you know is interested in participating, get full contest details here.
Teachers, get resources about how to engage your students in the contest here.
Time Series with Matrix Profile
Enough talking, so what is a Matrix Profile? Why should you care about it?
Matrix Profile
If you are here, you are likely aware of what a Distance Matrix (DM) is. If not, think about those tables that used to be on maps with the distance between cities. It is widely used in TS for clustering, classification, motif search, etc. However, even for modestly sized datasets, the algorithms can take months to compute it and even with speed-up techniques (i.e., indexing, lower-bounding, early abandoning) they can be, at best, one or two orders of magnitude faster. Matrix Profile it’s like a DM but faster (much faster) to compute. Figure 1 shows a DM and a Matrix Profile. As you can see, in the Matrix Profile, as the name suggests, you see the Profile of a DM. It stores the minimum Euclidean distance of every subset of one TS (think of a Sliding Window) with another (or itself, called Self-Join). It also stores a companion vector called Profile Index, that gives us the index of each nearest neighbor.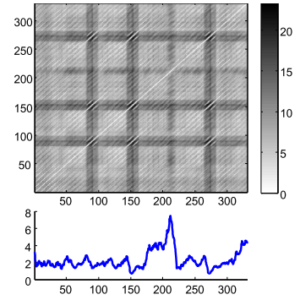
Why should you care?
DM usually stores redundant information, useless for most TS applications. The Matrix Profile has a host of interesting and exploitable properties. For example, the highest point on the Matrix Profile corresponds to the TS discord, the (tied) lowest points correspond to the locations of the best TS motif pair, and the variance can be seen as a measure of the TS complexity. Moreover, the histogram of the values in the Matrix Profile is the exact answer to the TS density estimation. Particularly, it has implications for TS motif discovery, TS joins, shapelet discovery (classification), density estimation, semantic segmentation, visualization, rule discovery, clustering, etc.1This method has the following advantages/features:
- It is exact, providing no false positives or false dismissals.
- It is simple and parameter-free. In contrast, the more general metric space APSS2 algorithms require building and tuning spatial access methods and/or hash functions.
- It requires an inconsequential space overhead, just O(n) with a small constant factor.
- It is extremely scalable, and for massive datasets, we can compute the results in an anytime fashion, allowing ultra-fast approximate solutions.
- Having computed the similarity join for a dataset, we can incrementally update it very efficiently. In many domains, this means we can effectively maintain exact joins on streaming data forever.
- It provides full joins, eliminating the need to specify a similarity threshold, which is a near-impossible task in this domain.
- It is embarrassingly parallelizable, both on multicore processors and in distributed systems.
Performance on an Intel(R) Core(TM) i7-7700 CPU @ 3.60GHz using a random walk dataset
set.seed(2018) data <- cumsum(sample(c(-1, 1), 40000, TRUE))
| Elapsed Time3 | Data size | Window size | Threads | |
|---|---|---|---|---|
| scrimp() | 45.30s | 40000 | 1000 | 1 |
| stomp_par() | 52.72s | 40000 | 1000 | 8 |
| stomp() | 136.01s | 40000 | 1000 | 1 |
| stamp_par() | 140.25s | 40000 | 1000 | 8 |
| stamp() | 262.03s | 40000 | 1000 | 1 |
Further readings
All information you need to get started with Matrix Profiles is available at the UCR Matrix Profile webpage. Papers, Slides, examples, are available there. Once become more familiar with this concept, you can start reading the TSMP R Package documentation.- For pure similarity search, it is suggested you see MASS for Euclidean Distance and the UCR Suite for DTW.
- All Pairs Similarity Search.
- These are results using only R code, no low-level C code optimizations.
Save On an Annual DataCamp Subscription (Less Than 2 Days Left)

DataCamp is now offering a discount on unlimited access to their course curriculum. Access over 170+ course in R, Python, SQL and more taught by experts and thought-leaders in data science such as Mine Cetinkaya-Rundel (R-Studio), Hadley Wickham (R-Studio), Max Kuhn (caret) and more. Check out this link to get the discount!
Below are some of the tracks available. You can choose a career track which is a deep dive into a subject that covers all the skills needed. Or a skill track which focuses on a specific subject.
Tidyverse Fundamentals (Skill Track)
Experience the whole data science pipeline from importing and tidying data to wrangling and visualizing data to modeling and communicating with data. Gain exposure to each component of this pipeline from a variety of different perspectives in this tidyverse R track.
Finance Basics with R (Skill Track) If you are just starting to learn about finance and are new to R, this is the right track to kick things off! In this track, you will learn the basics of R and apply your new knowledge directly to finance examples, start manipulating your first (financial) time series, and learn how to pull financial data from local files as well as from internet sources.
Data Scientist with R (Career Track)
A Data Scientist combines statistical and machine learning techniques with R programming to analyze and interpret complex data. This career track gives you exposure to the full data science toolbox.
Quantitative Analyst with R (Career Track)
In finance, quantitative analysts ensure portfolios are risk balanced, help find new trading opportunities, and evaluate asset prices using mathematical models. Interested? This track is for you.
And much more – the offer ends September 25th so don’t wait!
About DataCamp:
DataCamp is an online learning platform that uses high-quality video and interactive in-browser coding challenges to teach you data science using R, Python, SQL and more. All courses can be taken at your own pace. To date, over 2.5+ million data science enthusiasts have already taken one or more courses at DataCamp.
Simple Steps to Create Treemap in R
A treemap is a diagram representing hierarchical data in the form of nested rectangles, the area of each corresponding to its numerical value
When not to use a treemap
A treemap should not be used when there is a big difference between the measure values or the values are not comparable. Also, negative values cannot be displayed on a treemap. Building a Treemap in R To create a treemap we use one or more dimension and a maximum of 2 measures. We will be using the treemap package in R. For this article we will use the Super Store data which is provided along with the article. Step 1: Importing Data and installing treemap package in R## Set the working directory location to the file location##
>setwd("H:/R Treemap")
## Import the datafile in R and view the data sample)
>data= read.csv("data.csv", header = TRUE, sep =",")
>View(data)
Once we get the data in R we need to load the package treemap so that we can go ahead creating our required plot.
## Installing the package and calling the package in R##
>install.packages("treemap")
>library(treemap)
The data that we are using is already reshaped data and so we can go ahead with creating our basic treemap and move step by step from it.
Step 2: Creating a Treemap
The treemap function is used to create a treemap.
## Creating the most basic treemap##
>treemap(data,index = c("Category"),vSize ="Sales")
The first argument in the above formula is the data file name which is “data” in our case. The arguments within the index specify the hierarchy that we are looking into and the argument vSize tell R to pick up a values on which the proportion of the boxes are to be decided.
In our case since we have only index in our formula the command just splits the entire tree in three parts ( each representing the proportion of Sales for these part)
A first look into the above figures shows that the Proportion of Technology, Furniture and Office Supplies is almost within the same range , the highest being technology.
We can check our hunch right away, Type in the following :
>aggregate(Sales ~ Category, data, sum)
And you will get the following result :
Category Sales
1 Furniture 741999.8
2 Office Supplies 719047.0
3 Technology 836154.0
We see how close these Sales are to other (proportionately)
Now as we have created our most basic treemap lets go a bit further and see what happens when we list multiple values in the index ( create a hierarchy )
## Creating a treemap with Category and Subcategory as a hierarchy.
>treemap(data,index = c("Category","Sub.Category"),vSize = "Sales")
Here is what happened, the tree is first splits at the category level and then each category further splits under a subcategory. We can see from the treemap that the Technology Category accounted for maximum sales and within the Technology category, Phones accounted for most of the sales. (the size of the boxes are still by Sales)
Let’s go a step further and color the boxes by another measure let’s say profit.
##Coloring the boxes by a measure##
>treemap(data,index = c("Category","Sub.Category"),vSize ="Sales",vColor = "Profit",type="value")
The treemap that we get here is similar to the previous one except for the fact that now the box color represents the Profit instead. So we can see here that the most profitable subcategory was Copiers while on the other hand Tables were the most unprofitable.
The argument vColor tells R to pick up a variable that we want to be used as a color. Type Defines if it is a value, index or categorical.
##Using a categorical variable as color##
>treemap(data,index = c("Category","Region"),vSize ="Sales",vColor = "Region",type="categorical")
Here we see that the tree is split into Categories first and under each category we have all the four region that are distinguished by individual color.
Step 3: Enhancing our treemap
Let’s move ahead and make our treemap more readable. To do this we will add a title to our treemap and change to font size of the Labels for category and Subcategories. We will try to keep the labels for Categories bigger and sub categories a bit smaller. Here’s how to do it:
## Titles and font size of the labels##
>treemap(data,index = c("Category","Sub.Category"),vSize ="Sales",vColor = "Profit",type="value",title = "Sales Treemap For categories",fontsize.labels = c(15,10))
Notice how we have added a custom title to treemap and change the label size for Categories and Sub categories. The argument title allows us to add title to our visual while the argument fontsize.labels helps in adjusting the size of the labels.
How about positioning the labels ??
How about keeping the Categories labels centered and keeping that of Sub Categories in top left.
This can be achieved by the argument align.labels as under:
## Aligning the labels##
>treemap(data,index = c("Category","Sub.Category"),vSize ="Sales",vColor = "Profit",type="value",title = "Sales Treemap For categories",fontsize.labels = c(15,10),align.labels = list(c("centre","centre"),c("left","top")))
There it is, our labels are now aligned beautifully.
We can also choose our custom palette for treemaps using the palette argument as under:
>treemap(data,index = c("Category","Sub.Category"),vSize ="Sales",vColor = "Profit",type="value",palette="RdYlGn",range=c(-20000,60000),mapping=c(-20000,10000,60000),title = "Sales Treemap For categories",fontsize.labels = c(15,10),align.labels = list(c("centre","centre"),c("left","top")))
Here we have used the custom Red Yellow Green palette to see the profit more clearly.
Red being the most unprofitable and Green being the most profitable. In this article we looked upon how to create a treemap in R and adding aesthetic to our plot. There’s much more that can be done using the arguments under a treemap. For a complete list of argument and functionality refer the package documents.
“Area-based visualizations have existed for decades. This idea was invented by professor Ben Shneiderman at the University of Maryland, Human – Computer Interaction Lab in the early 1990s. Shneiderman and his collaborators then deepened the idea by introducing a variety of interactive techniques for filtering and adjusting treemaps. These early treemaps all used the simple “slice-and-dice” tiling algorithm”.
Treemaps are the most efficient option to display hierarchy that gives a quick overview of structure. They are also great at comparing the proportion between categories via their area sizes.
Author Bio:
This article was contributed by Perceptive Analytics. Rahul Singh, Chaitanya Sagar, Jyothirmayee Thondamallu and Saneesh Veetil contributed to this article. Perceptive Analytics provides data analytics, data visualization, business intelligence and reporting services to e-commerce, retail, healthcare and pharmaceutical industries. Our client roster includes Fortune 500 and NYSE listed companies in the USA and India.Reproducible development with Rmarkdown and Github
Github
While data science processes usually don’t involve the exact same workflows like software development (for which Git was originally intended) I think Git is actually very well suited to the iterative nature of data-science tasks. When walking down different avenues in the exploration path, it’s worth while to have them reside in different branches. That way instead of jotting down in general pointers what you did along with some code snippets in some text file (or god-forbid word when you want to have images as well) you can instead go back to the relevant branch, see the different iterations and read a neat report with code and images. You can even re-visit ideas that didn’t make it into the master branch. Be sure to use informative branch names and commit messages!Below is in illustration of how that process might look like:
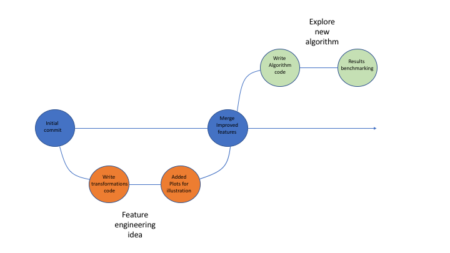
Using Github allows one to easily package his code, supporting files etc (using repos) and share it with fellow researches, which can in turn clone the repo, re-run the code and go through all the development iterations without a hassle.
Rmarkdown
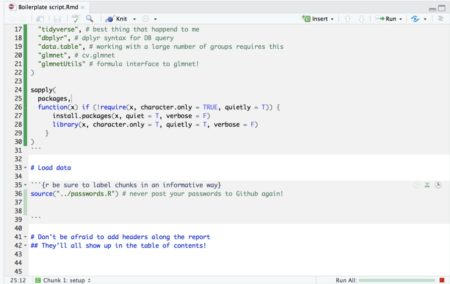
Most people familiar with Rmarkdown know it’s a great tool to write neat reports in all sorts of formats (html, PDF and even word!). One format that really makes it a great combo with Github is the github_document format. While one can’t view HTML files on Github, the output file from a github_document knit is an .md file which renders perfectly well on github, supporting images, tables, math, table of contents and many other. What some may not realize is that Rmarkdown is also a great development tool in itself. It behaves much like the popular Jupiter notebooks, with plots, tables and equations showing next to the code that generated them. What’s more, it has tons of cool features that really support reproducible development such as:- The first r-chunk (labled “setup” in the Rstudio template) always runs once when you execute code within chunks following it (pressing ctrl+Enter). It’s handy to load all packages used in later chucks (I like installing missing ones too) in this chunk such that whenever you run code within any of the chunks below it the needed packages are loaded.
- When running code from within a chunk (pressing ctrl+Enter) the working directory will always be the one which the .Rmd file is located at. In short this means no more worrying about setting the working directory – be it when working on several projects simultaneously or when cloning a repo from Github.
- It has many cool code execution tools such as a button to run code in all chunks up to the current one, run all code in the current chunk and it has a green progress bar so you don’t get lost too!
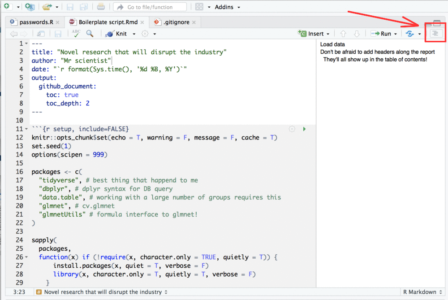
- If your script is so long that scrolling around it becomes tedious, you can use this neat feature in Rstudio: When viewing Rmarkdown files you can view an interactive table of contents that enables you to jump between sections (defined by # headers) in your code:
To summarize this section, I would highly recommend developing with Rmd files rather than R files.
A few set-up tips
- Place a file “passwords.R” with all passwords in the directory to which you clone repos and source it via the Rmd. That way you don’t accidentally publish your passwords to Github
- I like working with cache on all chunks in my Rmd. It’s usually good practice to avoid uploading the cache files generated in the process to Github so be sure to add to your .gitignore file the file types: *.RData, *.rdb, *.rdx, *.rds, *__packages
- Github renders CSV files pretty nicely (and enables searching them conveniently) so if you have some reference tables you want to include and you have a *.csv entry in your .gitignore file, you may want to add to your .gitignore the following entry: !reference_table_which_renders_nicely_on_github.csv to exclude it from the exclusion list.
Sample Reproducible development repo
Feel free to clone the sample reproducible development repo below and get your reproducible project running ASAP!https://github.com/IyarLin/boilerplate-script
Using Control Charts in R
I am sure you must have heard of Six Sigma quality standard or Six Sigma experts. But, what is Six Sigma?
Six Sigma is a set of techniques used by organizations to improve their processes and optimize operations. Six Sigma was popularized by manufacturing organizations and Jack Welch, former CEO of GE, was one of advocators of Six Sigma. At the heart of Six Sigma lies the core strategies to improve the quality of processes by identifying and removing the causes leading to defects and variability in product quality and business processes. Six Sigma uses empirical and statistical quality management methods to carry out operational improvement and excellence projects in organizations.
Six Sigma projects follow methodologies which are called as DMAIC and DMADV. DMAIC methodology is used for projects aimed at improving existing business processes; while, DMADV is used for projects which aims at creating new processes. Since this article talks about control charts, we will focus on DMAIC project methodology of which control charts is a part of. DMAIC methodology has five phases:
- Define
- Measure
- Analyze
- Improve
- Control
Define
Defining the goals that you wish to achieve – basically, identifying the problem statement you are trying to solve. In this stage, everyone involved in the project understands his/her role and responsibilities. There should be clarity on ‘Why is the project being undertaken?’
Measure
Understanding the ‘As-Is’ state of the process. Based on the goal defined in the ‘Define’ phase, you understand the process in detail and collect relevant data which is to be used in subsequent phases.
Analyze
By this phase, you know the goal that are you trying to achieve and also, you understand the entire process and have the relevant data to diagnose and analyze the problem. In this phase, make sure that your biases don’t lead you to results. Instead, it should be a complete fact-based and data-driven exercise to identify the root cause.
Improve
Now, you are aware about the entire process and cause behind the problems. In this phase, you need to find out ways or methodologies to work on the problem and improve the current processes. You have to think of new ways using techniques such as design of experiments and set up pilot projects to test the idea.
Control
You have implemented new processes and now, you have to ensure that any deviations in the optimized processes are corrected before they result in any defects. One of the techniques that can be used in control phase is statistical process control. Statistical process control can be used to monitor the processes and ensure that the desired quality level is maintained.
Control chart is the primary statistical process control tool used to monitor the performance of processes and ensure that they are operating within the permissible limits. Let’s understand what are control charts and how are they used in process improvement.
According to Wikipedia, “The data from measurements of variations at points on the process map is monitored using control charts. Control charts attempt to differentiate “assignable” (“special”) sources of variation from “common” sources. “Common” sources, because they are an expected part of the process, are of much less concern to the manufacturer than “assignable” sources. Using control charts is a continuous activity, ongoing over time.”
Let’s take an example and understand it step by step using above definition. You leave for office from your home every day at 9:00 AM. The average time it takes you to reach office is 35 minutes; while in most of the cases it takes 30 to 40 minutes for you to reach office. There is a variation of 5 minutes less or more because of slight traffic or you get all the traffic signals red on your way. However, on one fine day you leave from your home and you reach office in 60 minutes because there was an accident on the way and the entire traffic was diverted which caused additional delay of around 20 minutes. Now, relating our example with the definition above:
Measurements: Time to reach office – the time taken on daily basis to reach office from home is measured to monitor the system/process.
Variations: Deviations from the average time of 35 minutes – these variations are due to inherent attributes in the system such as traffic or traffic signals on the route.
Common sources: Slight traffic or traffic signals on the route – these are usually part of the processes and are of much less concern while driving to office.
Excessive Variation: Accident – these are events which leads to variations in the processes, leading to defects in the outputs or delayed processes.
Summing up everything, control charts are graphical techniques to monitor the performance of a process over time. In the control chart, the performance of these processes is monitored visually to identify any anomalies or variations from the usual behavior. For every control chart, there are control limits or decision limits set which define the normal behavior of the process. Any movement outside those limits indicate variation in the process and needs to be corrected to prevent further damage.
In any control chart, there are three main attributes – Average Line, UCL and LCL. Average line is the mean of all the observations taken in the process. UCL and LCL are upper control limit and lower control limit, respectively. These limits define the control or decision limits within which a process should always fall for efficient and optimized operations. These three values are determined by the process. For a process where all the values lie within the control limits and there is no specific pattern in the values, the process is said to be “in-control.”
X-axis can have either time or sample sequence; while, the Y-axis can have individual values or deviations. There are different control charts based on the data you have, continuous or variable (height, weight, density, cost, temperature, age) and attribute (number of defective parts produced). Accordingly, you choose the control chart and control objective.
Following steps present the step-by-step approach to implement a control chart:
- What process needs to be controlled?
Answer to this question will come from the DMAIC process while implementing the entire project methodology.
- Which system will provide the data to monitor?
Identifying the systems that will provide the data based on which control charts will be prepared and monitored.
- Develop and monitor control charts
Develop the control charts by specifying the X-axis and Y-axis.
- What actions to take based on control charts?
Once you have developed control charts, you need to monitor the processes and check for any special or excessive variations which may lead to defects in the processes.
By now, we have understood what control charts are and what information do they provide. Let us understand further uses of control charts and what more information can be extracted from these charts. Apart from manufacturing, control charts find their applications in healthcare industry and a host of other industries.
- Control charts provide a very simple and easy to understand methodology to understand the performance of processes.
- It reduces the need for inspection – the need for inspection arises only when the process behavior is significantly different from the usual behavior.
- If changes have been made to the process, control charts can help in understanding the impact of those changes on desired results.
- The data collected in the process can be used for improvement in the subsequent of follow-up projects
Control Chart Rules
For a process ‘in-control’, most of the points should lie near the average line i.e. Zone A, followed by Zone B and Zone C. Very few points should lie close to control limits and none of the points should fall beyond the control limits. There are eight rules which are helpful in identifying if there are certain patterns or special causes of variation in the observations.
Rule 1: One or more points beyond the control limits
Rule 2: 8 out of 9 points on the same side of the center line (Average line)
Rule 3: 6 consecutive points increasing or decreasing (monotonic)
Rule 4: 14 consecutive points are alternating up and down
Rule 5: 2 out of 3 consecutive points in Zone C or beyond
Rule 6: 4 out of 5 consecutive points in Zone B or beyond
Rule 7: 15 consecutive points are in Zone A
Rule 8: 8 consecutive points on either side of the Average line but not in Zone A
Now, we have understood the control charts, attributes, applications and associated rules, let’s try to implement a small example in R.
Let’s assume that there is a company which manufactures cylindrical piston rings. For each of the rings manufactured, measurement of the diameter is taken 5 times and captured to examine the within piece variability. These five measurements for one-piece forms one sample or one sub-group. Similarly, measurements for 25 pieces is taken. Using rnorm function in R, let’s create the measurement values.
| > obs V1 V2 V3 V4 V5 1 1.448786 1.555614 1.400382 1.451316 1.328760 2 1.748518 1.525284 1.552703 1.417736 1.420078 3 1.600783 1.409819 1.350917 1.521953 1.358915 4 1.529281 1.582439 1.544136 1.712162 1.553276 5 1.479104 1.343972 1.642736 1.589858 1.460230 6 1.685809 1.553799 1.493372 1.609255 1.471565 7 1.493397 1.373165 1.660502 1.535789 1.512498 8 1.483724 1.564052 1.415218 1.436863 1.578013 9 1.480014 1.446424 1.604218 1.565367 1.412440 10 1.530056 1.398036 1.469385 1.667835 1.384063 11 1.423609 1.419212 1.420791 1.347140 1.485413 12 1.508196 1.505683 1.642166 1.559233 1.332157 13 1.574303 1.595021 1.484574 1.375992 1.367742 14 1.491598 1.387324 1.486832 1.372965 1.444112 15 1.420711 1.479883 1.411519 1.377991 1.251022 16 1.407785 1.477150 1.671345 1.562293 1.617919 17 1.586156 1.555872 1.515936 1.498874 1.579370 18 1.700294 1.574875 1.710501 1.544640 1.660743 19 1.593655 1.691820 1.470600 1.479399 1.506595 20 1.338427 1.600721 1.434118 1.541265 1.602901 21 1.442494 1.825335 1.450115 1.493083 1.433342 22 1.499603 1.483825 1.479840 1.466675 1.465325 23 1.432389 1.533376 1.456744 1.460206 1.456417 24 1.395037 1.382133 1.460687 1.449885 1.305300 25 1.445672 1.607760 1.534657 1.422726 1.416209 |
| > qq = qcc(obs, type = “R”, nsigmas = 3) |
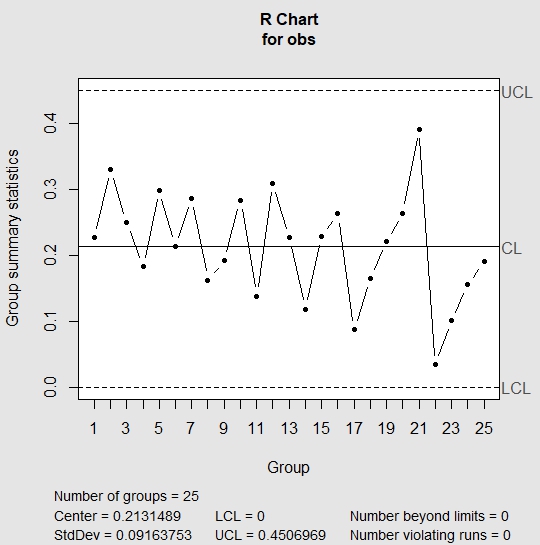
In R chart, we look for all rules that we have mentioned above. If any of the above rules is violated, then R chart is out of control and we don’t need to evaluate further. This indicates the presence of special cause variation. If the R chart appears to be in control, then we check the run rules against the X-Bar chart. In the above chart, R chart appears to be in control; hence, we move to check run rules against the X-Bar chart.
| > summary(qq) Call: qcc(data = obs, type = “R”, nsigmas = 3) R chart for obs Summary of group statistics: Min. 1st Qu. Median Mean 3rd Qu. Max. 0.0342775 0.1627947 0.2212205 0.2131489 0.2644740 0.3919933 Group sample size: 5 Number of groups: 25 Center of group statistics: 0.2131489 Standard deviation: 0.09163753 Control limits: LCL UCL 0 0.4506969 |
| > qq = qcc(obs, type = “xbar”, nsigmas = 3) |
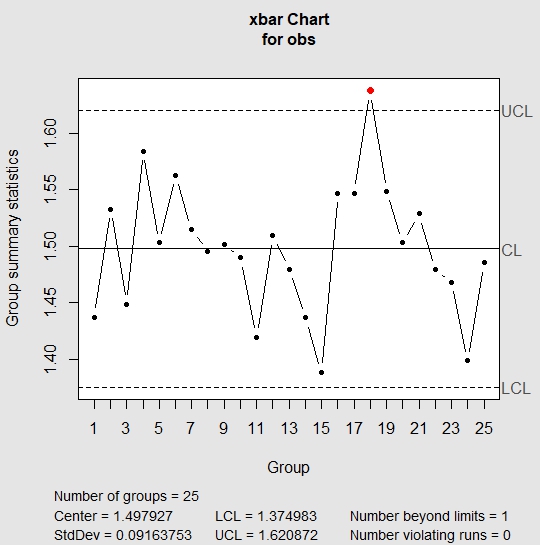
In the above chart, one of the points lie outside the UCL which implies that the process is out of control. The standard deviation in the above chart is the standard deviation of means of each of the samples. If we were to look at the sample 18, we see that the values in sample 18 are usually higher than values in other samples.
| > obs[18,] V1 V2 V3 V4 V5 18 1.700294 1.574875 1.710501 1.54464 1.660743 |
Now, let’s check process capability. By process capability, we can check if control limits and specification limits are in sync with each other. For instance, in the case we have taken, our client wanted piston rings with target diameter of 1.5 cm with a variation of +/- 0.1 cm. Process capability will help us in identifying whether our system is capable to meeting the specified requirements. It is measured by process capability index Cpk.
| > process.capability(qq, spec.limits = c(1.4,1.6)) Process Capability Analysis Call: process.capability(object = qq, spec.limits = c(1.4, 1.6)) Number of obs = 125 Target = 1.5 Center = 1.498 LSL = 1.4 StdDev = 0.09164 USL = 1.6 Capability indices: Value 2.5% 97.5% Cp 0.3638 0.3185 0.4089 Cp_l 0.3562 0.2947 0.4178 Cp_u 0.3713 0.3088 0.4338 Cp_k 0.3562 0.2829 0.4296 Cpm 0.3637 0.3186 0.4087 Exp<LSL 14% Obs<LSL 15% Exp>USL 13% Obs>USL 16% |
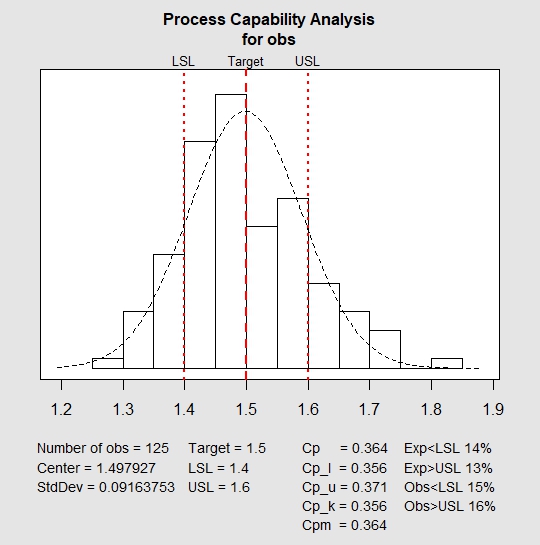
In the above plot, red lines indicate the target value, the lower and upper specified range. It can easily be inferred that the system is not capable to manufacture products within the specified range. Also, for a capable process, value of Cpk should be greater than or equal to 1.33. In the above chart, the value is 0.356 which is less than the required value. This shows that the above process is neither stable nor capable.
I am sure after going through this article, you will be able to use and create control charts in multiple other cases in your work. We would love to hear your experience with creating control charts in different settings.
Author Bio:
This article was contributed by Perceptive Analytics. Jyothirmayee Thondamallu, Chaitanya Sagar and Saneesh Veetil contributed to this article.
Perceptive Analytics is a marketing analytics company and it also provides Tableau Consulting, data analytics, business intelligence and reporting services to e-commerce, retail, healthcare and pharmaceutical industries. Our client roster includes Fortune 500 and NYSE listed companies in the USA and India.