The Best Algorithms are the Simplest
The field of data science has progressed from simple linear regression models to complex ensembling techniques but the most preferred models are still the simplest and most interpretable. Among them are regression, logistic, trees and naive bayes techniques. Naive Bayes algorithm, in particular is a logic based technique which is simple yet so powerful that it is often known to outperform complex algorithms for very large datasets. Naive bayes is a common technique used in the field of medical science and is especially used for cancer detection. This article explains the underlying logic behind naive bayes algorithm and example implementation.How Probability defines Everything
We calculate probability as the proportion of cases where an event happens and call it the probability of the event. Just as there is probability for a single event, we have probability of a group of events as the proportion of cases where the group of events occur together. Another concept in probability is calculating the occurrence of events in a particular sequence, that is, if it is known that something has already happened, what will be the probability that another event happens after that. By logic, one can understand that we are narrowing down our scope to only the case when that something has already happened and then calculating the proportion of cases where our second event occurs. To represent it mathematically, If A is the first event and B is the second event, then P(B|A) is our desired probability of calculating probability of event A after occurrence of event B, P(A n B) is probability of the two events occurring togetherP(B | A) = P(B) * P(A | B) / P(A)
This is the foundation pillar for Naive bayes algorithm. Owing to this, Naive Bayes can handle different kind of events which are differentiated by the probabilities of event separately, that is , P(B) and conditional probability P(B|A). If the two probabilities are same, then it means that the occurrence of event A had no effect on event B and the events are known as independent events. If the conditional probability becomes zero, then it means the occurrence of event A implies that event B cannot occur. If the reverse is also true, then the events are known as mutually exclusive events and the occurrence of only one of the events at a time is possible. All other cases are classified as dependent events where the conditional probability can be either lower or higher than the original. In real life, every coin toss is independent of all other coin tosses made previously and thus coin tosses are independent. The outcome of a single coin toss is composed of mutually exclusive events. We cannot have a head and the tails at the same time. When we consider runs of multiple coin tosses, we are talking about dependent events. For a combination of three coin tosses, the final outcome is dependent of the first, second as well as the third coin toss.
How do we Calculate these Probabilities?
It is easy to calculate the probability of a single event. It equates to the number of cases when the event occurs divided by the total number of possible cases. For instance, the probability of a 6 in a single six-faced die roll is ⅙ if all the sides have equal chance of coming. However, one needs to be careful when calculating probabilities of two or more events. Simply knowing the probability of each event separately is not enough to calculate the probability of multiple events happening. If we additionally know that the events are independent, then the probability of them occurring together is the multiplication of each event separately.We denote this mathematically as follows: P(A and B)=P(A)*P(B) – For independent events
As I already described, each coin toss is independent of other coin tosses. So the probability of having a Heads and a Heads combination in two coin tosses is P(Heads-Heads Combo)=P(Heads in first throw)*P(Heads in second throw)=½ * ½ = ¼
If the events are not independent, we can use the probability of any one event multiplied by the probability of second event after the first has happened
P(A and B)=P(A)*P(B|A) – For dependent events
An example of dependent events can be drawing cards without replacement. If you want to know that the two cards drawn are King and Queen then we know that the probability of the first event is dependent of 52 cards whereas the probability of the second event is dependent on 51 cards.
Thus, P(King and Queen)=P(King)*P(Queen|King)
Here, P(King) is 4/52. After a King is drawn, there are 4 queens out of 51 cards. So, P(Queen|King) is 4/51 P(King and Queen)=4/52*4/51=~0.6%
This is known as general multiplication rule. It also applies to the independent events scenario but since the events are independent, P(B|A) becomes equal to P(B)
The third case is for mutually exclusive events. If the events are mutually exclusive, we know that only one of the events can occur at a time. So the probability of the two events occurring together is zero. We are sometimes interested in probability of one of the events occuring and it is the sum of the individual probabilities in this scenario.
P(A OR B)=P(A)+P(B) – for mutually exclusive events
If we’re talking about a single six faced fair die throw, the probability of any two numbers occurring together is zero. In this case the probability of any prime number occuring is the sum of occurrence of each prime number. In this case P(2)+P(3)+P(5)
Had the events not been mutually exclusive, the probability of one of the events would have counted the probability of both events coming together twice. Hence we subtract this probability. P(A OR B)=P(A)+P(B)-P(A AND B) – for events which are not mutually exclusive
In a single six faced fair dice throw, the probability of throwing a multiple of 2 or 3 describes a scenario of events which are not mutually exclusive since 6 is both a multiple of 2 and 3 and is counted twice.
Thus, P(multiple of 2 or 3)=P(Multiple of 2)+P(Multiple of 3)- P(Multiple of 2 AND 3) =P(2,4,6)+P(3,6)-P(6)=3/6 + 2/6 -1/6 = 4/6 =2/3
This is known as general addition rule and similar to the multiplication rule, it also applies to the mutually exclusive events scenario but in that case, P(A AND B) is zero.
This is all we need to understand how Naive Bayes algorithm works. It takes into account all such scenarios and learns accordingly. Let’s get our hands dirty with a sample dataset.
Naive Bayes – a Not so Naive Algorithm
The reason that Naive Bayes algorithm is called Naive is not because it is simple or stupid. It is because the algorithm makes a very strong assumption about the data having features independent of each other while in reality, they may be dependent in some way. In other words, it assumes that the presence of one feature in a class is completely unrelated to the presence of all other features. If this assumption of independence holds, Naive Bayes performs extremely well and often better than other models. Naive Bayes can also be used with continuous features but is more suited to categorical variables. If all the input features are categorical, Naive Bayes is recommended. However, in case of numeric features, it makes another strong assumption which is that the numerical variable is normally distributed.R supports a package called ‘e1071’ which provides the naive bayes training function. For this demonstration, we will use the classic titanic dataset and find out the cases which naive bayes can identify as survived.
The Titanic dataset in R is a table for about 2200 passengers summarised according to four factors – economic status ranging from 1st class, 2nd class, 3rd class and crew; gender which is either male or female; Age category which is either Child or Adult and whether the type of passenger survived. For each combination of Age, Gender, Class and Survived status, the table gives the number of passengers who fall into the combination. We will use the Naive Bayes Technique to classify such passengers and check how well it performs. As we know, Bayes theorem is based on conditional probability and uses the formula
P(A | B) = P(A) * P(B | A) / P(B)
We now know how this conditional probability comes from multiplication of events so if we use the general multiplication rule, we get another variation of the theorem that is, using P(A AND B) = P(A) * P(B | A), we can obtain the value for conditional probability: P(B | A) = P(A AND B) / P(A) which is the variation of Bayes theorem.
Since P(A AND B) also equals P(B) * P(A | B), we can substitute it and get back the original formula P(B | A) = P(B) * P(A | B) / P(A) Using this for each of the features among Age, Gender and Economic status, Naive Bayes algorithm will calculate the conditional probability of survival of the combination
#Getting started with Naive Bayes #Install the package #install.packages(“e1071”) #Loading the library library(e1071) ?naiveBayes #The documentation also contains an example implementation of Titanic dataset #Next load the Titanic dataset data(“Titanic”) #Save into a data frame and view it Titanic_df=as.data.frame(Titanic)We see that there are 32 observations which represent all possible combinations of Class, Sex, Age and Survived with their frequency. Since it is summarised, this table is not suitable for modelling purposes. We need to expand the table into individual rows. Let’s create a repeating sequence of rows based on the frequencies in the table
#Creating data from table repeating_sequence=rep.int(seq_len(nrow(Titanic_df)), Titanic_df$Freq) #This will repeat each combination equal to the frequency of each combination #Create the dataset by row repetition created Titanic_dataset=Titanic_df[repeating_sequence,] #We no longer need the frequency, drop the feature Titanic_dataset$Freq=NULLThe data is now ready for Naive Bayes to process. Let’s fit the model
#Fitting the Naive Bayes model Naive_Bayes_Model=naiveBayes(Survived ~., data=Titanic_dataset) #What does the model say? Print the model summary Naive_Bayes_ModelNaive Bayes Classifier for Discrete Predictors
Call:
naiveBayes.default(x = X, y = Y, laplace = laplace)
A-priori probabilities:
Y
No Yes
0.676965 0.323035
Conditional probabilities:
Class
Y 1st 2nd 3rd Crew
No 0.08187919 0.11208054 0.35436242 0.45167785
Yes 0.28551336 0.16596343 0.25035162 0.29817159
Sex
Y Male Female
No 0.91543624 0.08456376
Yes 0.51617440 0.48382560
Age
Y Child Adult
No 0.03489933 0.96510067
Yes 0.08016878 0.91983122
The model creates the conditional probability for each feature separately. We also have the a-priori probabilities which indicates the distribution of our data. Let’s calculate how we perform on the data.
#Prediction on the dataset
NB_Predictions=predict(Naive_Bayes_Model,Titanic_dataset)
#Confusion matrix to check accuracy
table(NB_Predictions,Titanic_dataset$Survived)
NB_Predictions No Yes
No 1364 362
Yes 126 349
We have the results! We are able to classify 1364 out of 1490 “No” cases correctly and 349 out of 711 “Yes” cases correctly. This means the ability of Naive Bayes algorithm to predict “No” cases is about 91.5% but it falls down to only 49% of the “Yes” cases resulting in an overall accuracy of 77.8%
Conclusion: Can we Do any Better?
Naive Bayes is a parametric algorithm which implies that you cannot perform differently in different runs as long as the data remains the same. We will, however, learn another implementation of Naive Bayes algorithm using the ‘mlr’ package. Assuming the same session is going on for the readers, I will install and load the package and start fitting a model#Getting started with Naive Bayes in mlr #Install the package #install.packages(“mlr”) #Loading the library library(mlr)The mlr package consists of a lot of models and works by creating tasks and learners which are then trained. Let’s create a classification task using the titanic dataset and fit a model with the naive bayes algorithm.
#Create a classification task for learning on Titanic Dataset and specify the target feature
task = makeClassifTask(data = Titanic_dataset, target = "Survived")
#Initialize the Naive Bayes classifier
selected_model = makeLearner("classif.naiveBayes")
#Train the model
NB_mlr = train(selected_model, task)
The summary of the model which was printed in e3071 package is stored in learner model. Let’s print it and compare
#Read the model learned
NB_mlr$learner.model
Naive Bayes Classifier for Discrete Predictors
Call:
naiveBayes.default(x = X, y = Y, laplace = laplace)
A-priori probabilities:
Y
No Yes
0.676965 0.323035
Conditional probabilities:
Class
Y 1st 2nd 3rd Crew
No 0.08187919 0.11208054 0.35436242 0.45167785
Yes 0.28551336 0.16596343 0.25035162 0.29817159
Sex
Y Male Female
No 0.91543624 0.08456376
Yes 0.51617440 0.48382560
Age
Y Child Adult
No 0.03489933 0.96510067
Yes 0.08016878 0.91983122
The a-priori probabilities and the conditional probabilities for the model are similar to the one calculated by e3071 package as was expected. This means that our predictions will also be the same.
#Predict on the dataset without passing the target feature
predictions_mlr = as.data.frame(predict(NB_mlr, newdata = Titanic_dataset[,1:3]))
##Confusion matrix to check accuracy
table(predictions_mlr[,1],Titanic_dataset$Survived)
No Yes
No 1364 362
Yes 126 349
As we see, the predictions are exactly same. The only way to improve is to have more features or more data. Perhaps, if we have more features such as the exact age, size of family, number of parents in the ship and siblings then we may arrive at a better model using Naive Bayes.
In essence, Naive Bayes has an advantage of a strong foundation build and is very robust. I know of the ‘caret’ package which also consists of Naive Bayes function but it will also give us the same predictions and probability.
Author Bio:
This article was contributed by Perceptive Analytics. Madhur Modi, Chaitanya Sagar, Vishnu Reddy and Saneesh Veetil contributed to this article.Perceptive Analytics provides data analytics, data visualization, business intelligence and reporting services to e-commerce, retail, healthcare and pharmaceutical industries. Our client roster includes Fortune 500 and NYSE listed companies in the USA and India.
Here is the Complete Code (used in this article):
#Getting started with Naive Bayes
#Install the package
#install.packages(“e1071”)
#Loading the library
library(e1071)
?naiveBayes #The documentation also contains an example implementation of Titanic dataset
#Next load the Titanic dataset
data("Titanic")
#Save into a data frame and view it
Titanic_df=as.data.frame(Titanic)
#Creating data from table
repeating_sequence=rep.int(seq_len(nrow(Titanic_df)), Titanic_df$Freq) #This will repeat each combination equal to the frequency of each combination
#Create the dataset by row repetition created
Titanic_dataset=Titanic_df[repeating_sequence,]
#We no longer need the frequency, drop the feature
Titanic_dataset$Freq=NULL
#Fitting the Naive Bayes model
Naive_Bayes_Model=naiveBayes(Survived ~., data=Titanic_dataset)
#What does the model say? Print the model summary
Naive_Bayes_Model
#Prediction on the dataset
NB_Predictions=predict(Naive_Bayes_Model,Titanic_dataset)
#Confusion matrix to check accuracy
table(NB_Predictions,Titanic_dataset$Survived)
#Getting started with Naive Bayes in mlr
#Install the package
#install.packages(“mlr”)
#Loading the library
library(mlr)
#Create a classification task for learning on Titanic Dataset and specify the target feature
task = makeClassifTask(data = Titanic_dataset, target = "Survived")
#Initialize the Naive Bayes classifier
selected_model = makeLearner("classif.naiveBayes")
#Train the model
NB_mlr = train(selected_model, task)
#Read the model learned
NB_mlr$learner.model
#Predict on the dataset without passing the target feature
predictions_mlr = as.data.frame(predict(NB_mlr, newdata = Titanic_dataset[,1:3]))
##Confusion matrix to check accuracy
table(predictions_mlr[,1],Titanic_dataset$Survived)
 In this post, taken from the book
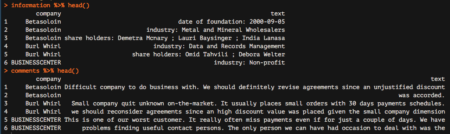
In this post, taken from the book  My plan was the following—get the information from these cards and analyze it to discover whether some kind of common traits emerge.
My plan was the following—get the information from these cards and analyze it to discover whether some kind of common traits emerge.
 Great! We are nearly done. We are now going to start analyzing the comments data frame, which reports all comments from our colleagues. The very last step needed to make this data frame ready for subsequent analyzes is to tokenize it, which basically means separating it into different rows for all the words available within the text column. To do this, we are going to leverage the unnest_tokens function, which basically splits each line into words and produces a new row for each word, having taken care to repeat the corresponding value within the other columns of the original data frame.
This function comes from the recent tidytext package by Julia Silge and Davide Robinson, which provides an organic framework of utilities for text mining tasks. It follows the tidyverse framework, which you should already know about if you are using the dplyr package.
Let’s see how to apply the unnest_tokens function to our data:
Great! We are nearly done. We are now going to start analyzing the comments data frame, which reports all comments from our colleagues. The very last step needed to make this data frame ready for subsequent analyzes is to tokenize it, which basically means separating it into different rows for all the words available within the text column. To do this, we are going to leverage the unnest_tokens function, which basically splits each line into words and produces a new row for each word, having taken care to repeat the corresponding value within the other columns of the original data frame.
This function comes from the recent tidytext package by Julia Silge and Davide Robinson, which provides an organic framework of utilities for text mining tasks. It follows the tidyverse framework, which you should already know about if you are using the dplyr package.
Let’s see how to apply the unnest_tokens function to our data:
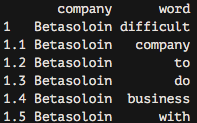 As you can see, we now have each word separated into a single record.
As you can see, we now have each word separated into a single record.