This represents Part 4 of a 4-part series relative to the calculation of Equity Cash Flow (ECF) using R. If you missed any of the prior posts, be certain to reference them before proceeding. Content in this section builds on previously described information/data. Part 3 of 4 prior post is located here – Part 3 of 4 .
‘ECF – Method 4’ differs slightly from the prior 3 versions. Specifically, it represents ECF with an adjustment. By definition, Equity Value (E) is calculated as the present value of a series of Equity Cash Flow (ECF) discounted at the appropriate discount rate, the cost of levered equity capital, Ke. When using forward rate discounting, the equation for E is as follows:
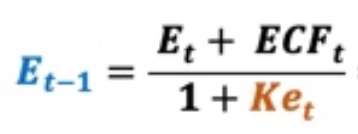
The cost of levered equity capital (Ke) is shown below.
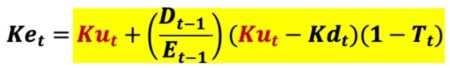
Where

Many DCF practitioners incorrectly assume the cost of equity capital (Ke) is constant in all periods. The above equation indicates Ke can easily vary over time even if Ku, Kd, and T are all constant values. Assuming a constant Ke value when such does not apply violates a basic premise of valuation, the value additivity rule, Debt Value (D) + Equity Value (E) = Asset Value (V). Substituting the cost of equity capital (Ke) into the Equity valuation (E) equation yield this.
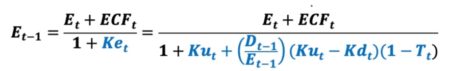
Note in the above valuation equation, equity value is a function of itself. We require Equity Value (E) in the prior period (t-1) in order to obtain the discount rate (Ke) for the current period “t.” This current period discount rate is used to calculate prior period’s equity value. This is clearly a circular calculation, as Equity Value (E) in the prior period (t-1) exists on both sides of the equation. While Excel solutions with intentional circular references such as this can be problematic, R experiences no such problems in proper iterative solution. Even so, we can completely bypass calculation circularity altogether and arrive at the correct iterative, circular solution. Using simple 8th grade math, a noncircular equity valuation equation is derived. Note this new noncircular equation requires a noncircular discount rate (Ku) and a noncircular numerator term in which to discount. All calculation circularity is eliminated in the equity valuation equation. The numerator includes a noncircular adjustment to Equity Cash Flow (ECF).

The 2 noncircular discount rates (Ku, Kd) are calculated using the Capital Asset Pricing Model (CAPM).

The noncircular debt valuation (D) equation using forward rate (Kd) discounting is provided below.

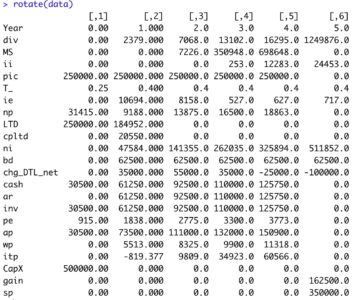
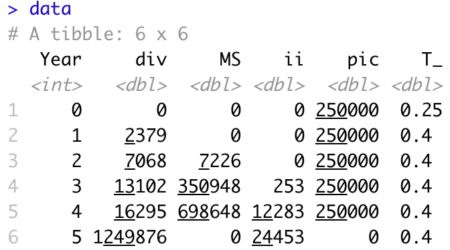
Reference Part 2 of 4 in this series for the calculation of debt cash flow (CFd). Update ‘data’ tibble
data <- data %>%
mutate(Rf = rep(0.03, 6),
MRP = rep(0.04, 6),
Bd = rep(0.2, 6),
Bu = rep(1.1, 6),
Kd = Rf + Bd * MRP,
Ku = Rf + Bu * MRP,
N = np + cpltd + LTD, # All interest bearing debt
CFd = ie - (N - lag(N, default=0)),
ECF3 = ni - ii*(1-T_) - ( Ebv - lag(Ebv, default=0) ) + ( MS - lag(MS, default=0)) )
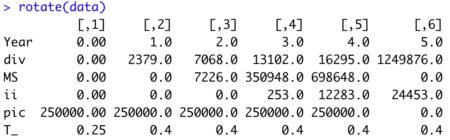
View tibblerotate(data)
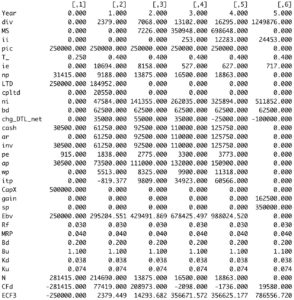
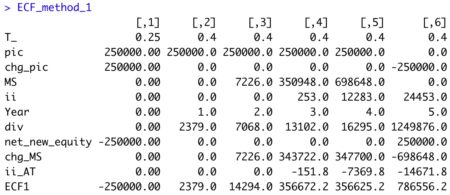
The R code below calculates Debt Value (D) and Equity Value (E) each period. The function sum these 2 values to obtain asset value (V).
R Code – ‘valuation’ R function
valuation <- function(a) {
library(tidyverse)
n <- length(a$bd) - 1
Rf <- a$Rf
MRP <- a$MRP
Ku <- a$Ku
Kd <- a$Kd
T_ <- a$T_
# Flow values
CFd <- a$CFd
ECF <- a$ECF3
# Initialize valuation vectors to zero by Year
d <- rep(0, n+1 ) # Initialize debt value to zero each Year
e <- rep(0, n+1 ) # Initialize equity value to zero each Year
# Calculate debt and equity value by period in reverse order using discount rates 'Kd' and 'Ku', repsectively
for (t in (n+1):2) # reverse step through loop from period 'n+1' to 2
{
# Debt Valuation discounting 1-period at the forward discount rate, Kd[t]
d[t-1] <- ( d[t] + CFd[t] ) / (1 + Kd[t] )
# Equity Valuation discounting 1-period at the forward discount rate, Ku[t]
e[t-1] <- ( e[t] + ECF[t] - (d[t-1])*(Ku[t]-Kd[t])*(1-T_[t]) ) / (1 + Ku[t] )
}
# Asset valuation by Year (Using Value Additivity Equation)
v = d + e
npv_0 <- round(e[1],0) + round(ECF[1],0)
npv_0 <- c(npv_0, rep(NaN,n) )
valuation <- as_tibble( cbind(a$Year, T_, Rf, MRP, Ku, Kd, Ku-Kd, ECF,
-lag(d, default=0)*(1-T_)*(Ku-Kd), ECF - lag(d, default=0)*(1-T_)*(Ku-Kd),
d, e, v, d/e, c( ECF[1], rep(NaN,n)), npv_0 ) )
names(valuation) <- c("Year", "T", "Rf", "MRP", "Ku", "Kd", "Ku_Kd", "ECF",
"ECF_adj", "ADJ_ECF", "D", "E", "V", "D_E_Ratio", "ECF_0", "NPV_0")
return(rotate(valuation))
}
View R output
valuation <- valuation( data ) round(valuation, 5)
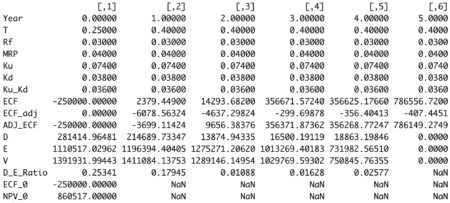
This method of noncircular equity valuation (E) is simple and straightforward. Unfortunately, DCF practitioners tend to incorrectly treat Ke as a noncircular calculation using CAPM. That widely used approach violates the value additivity rule.
Additionally, there is a widely held belief the Adjusted Present Value (APV) asset valuation approach is the only one that provides a means of calculating asset value in a noncircular fashion.
Citation: Fernandez, Pablo, (August 27, 2020), Valuing Companies by Cash Flow Discounting: Only APV Does Not Require Iteration.
Though the APV method is almost 50 years old, there is little agreement as to how to correctly calculate one of the model’s 2 primary components – the value of interest expense tax shields. The above 8th grade approach to equity valuation (E) eliminates the need to use the APV model for asset valuation if calculation by noncircular means is the goal. Simply sum the 2 noncircular valuation equations below (D + E). They ensure the enforcement of the value-additivity rule (V = D + E). Valuation Additivity Rule
(Assuming debt and equity are the 2 sources of financing)
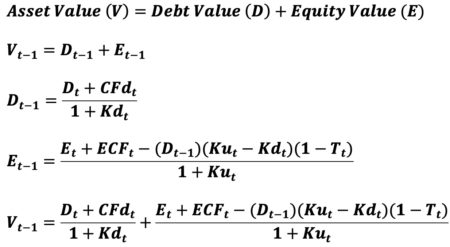 In summary, circular equity valuation (E) is entirely eliminated using simple 8th grade math. Adding this noncircular equity valuation (E) solution to noncircular debt valuation (D) results in noncircular asset valuation (V).
There is no need to further academically squabble over the correct methodology for valuing tax shields relative to the noncircular APV asset valuation model. Tax shields are not separately discounted using the above approach.
In summary, circular equity valuation (E) is entirely eliminated using simple 8th grade math. Adding this noncircular equity valuation (E) solution to noncircular debt valuation (D) results in noncircular asset valuation (V).
There is no need to further academically squabble over the correct methodology for valuing tax shields relative to the noncircular APV asset valuation model. Tax shields are not separately discounted using the above approach.This example is taken from my newly published textbook, ‘Advanced Discounted Cash Flow (DCF) Valuation using R.’ The above method is discussed in far greater detail, including the requisite 8th grade math, along with development of the integrated financials using R. Included in the text are 40+ advanced DCF valuation models – all of which are value-additivity compliant.
Typical corporate finance texts do not teach this very important concept. As a result, DCF practitioners often unknowingly violate the immensely important value-additivity rule. This modeling error is closely akin to violating the accounting equation (Book Assets = Book Liabilities + Book Equity) when constructing pro form balance sheets used in a DCF valuation.
For some reason, violation of the accounting equation is considered a valuation sin, while violation of the value-additivity rule is a well-established practice in DCF valuation land.
Reference my website for additional details.
https://www.leewacc.com/
Next up, 10 Different, Mathematically Equivalent Ways to Calculate Free Cash Flow (FCF) …
Brian K. Lee, MBA, PRM, CMA, CFA

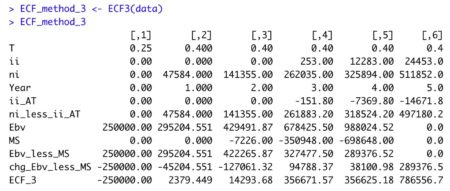
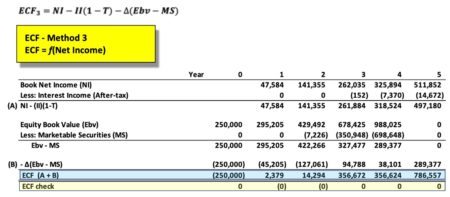
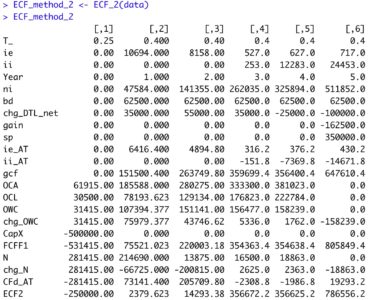
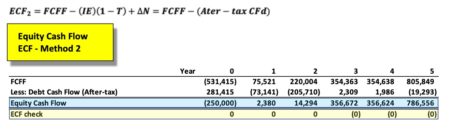
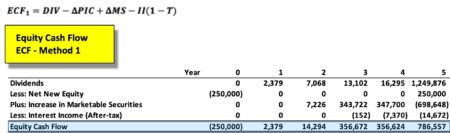
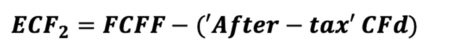 The equation appears innocent enough, though there are many underlying terms that require definition for understanding of the calculation. In words, ‘ECF – Method 2’ equals free cash Flow (FCFF) minus after-tax Debt Cash Flow (CFd).
The equation appears innocent enough, though there are many underlying terms that require definition for understanding of the calculation. In words, ‘ECF – Method 2’ equals free cash Flow (FCFF) minus after-tax Debt Cash Flow (CFd).