[This article was first published on the Azure Medium channel, and kindly contributed to R-bloggers]. (You can report issue about the content on this page here)
As probably you already know, Microsoft provided its Azure Machine Learning SDK for Python to build and run machine learning workflows, helping organizations to use massive data sets and bring all the benefits of the Azure cloud to machine learning.
Although Microsoft initially invested in R as the Advanced Analytics preferred language introducing the SQL Server R server and R services in the 2016 version, they abruptly shifted their attention to Python, investing exclusively on it. This basically happened for the following reasons:
- Python’s simple syntax and readability make the language accessible to non-programmers
- The most popular machine learning and deep learning open source libraries (such as Pandas, scikit-learn, TensorFlow, PyTorch, etc.) are deeply used by the Python community
- Python is a better choice for productionalization: it’s relatively very fast; it implements OOPs concepts in a better way; it is scalable (Hadoop/Spark); it has better functionality to interact with other systems; etc.
Azure ML Python SDK Main Key Points
One of the most valuable aspects of the Python SDK is its ease to use and flexibility. You can simply use just few classes, injecting them into your existing code or simply referring to your script files into method calls, in order to accomplish the following tasks:
- Explore your datasets and manage their lifecycle
- Keep track of what’s going on into your machine learning experiments using the Python SDK tracking and logging features
- Transform your data or train your models locally or using the best cloud computation resources needed by your workloads
- Register your trained models on the cloud, package them into container image and deploy them on web services hosted in Azure Container Instances or Azure Kubernetes Services
- Use Pipelines to automate workflows of machine learning tasks (data transformation, training, batch scoring, etc.)
- Use automated machine learning (AutoML) to iterate over many combinations of defined data transformation pipelines, machine learning algorithms and hyperparameter settings. It then finds the best-fit model based on your chosen performance metric.
In summary, the scenario is the following one:
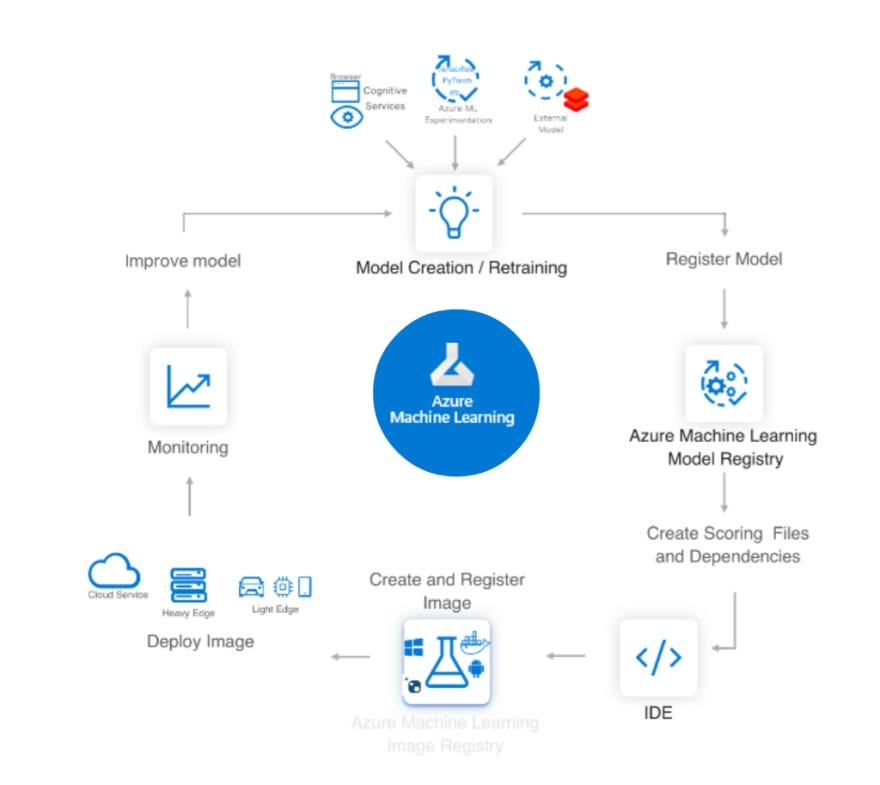
What About The R Community Engagement?
In the last 3 years Microsoft pushed a lot over the Azure ML Python SDK, making it a stable product and a first class citizen of the Azure cloud. But they seem to have forgotten all the R professionals who developed a huge amount of data science project all around the world.
We must not forget that in Analytics and Data Science the key of success of a project is to quickly try out a large number of analytical tools and find what’s the best one for the case in analysis. R was born for this reason. It has a lot of flexibility when you want to work with data and build some model, because it has tons of packages and easy of use visualization functionality. That’s why a lot of Analytics projects are developed using R by many statisticians and data scientists.
Fortunately in the last months Microsoft extended a hand to the R community, releasing a new project called Azure Machine Learning R SDK.
Can I Use R To Spin The Azure ML Wheels?
Starting from October 2019 Microsoft released a R interface for Azure Machine Learning SDK on GitHub. The idea behind this project is really straightforward. The Azure ML Python SDK is a way to simplify the access and the use of the Azure cloud storage and computation for machine learning purposes keeping the main code as the one a data scientist developed on its laptop.
Why not allow the Azure ML infrastructure to run also R code (using proper “cooked” Docker images) and let R data scientists call the Azure ML Python SDK methods using R functions?
The interoperability between Python and R is obtained thanks to reticulate. So, once the Python SDK module azureml is imported into any R environment using the import function, functions and other data within the azureml module can be accessed via the $ operator, like an R list.
Obviously, the machine hosting your R environment must have Python installed too in order to make the R SDK work properly.
Let’s start to configure your preferred environment.
Set Up A Development Environment For The R SDK
There are two option to start developing with the R SDK:
- Using an Azure ML Compute Instance (the fastest way, but not the cheaper one!)
- Using your machine (laptop, VM, etc.)
Set Up An Azure ML Compute Instance
Once you created an Azure Machine Learning Workspace through the Azure portal (a basic edition is enough), you can access to the brand new Azure Machine Learning Studio. Under the Compute section, you can create a new Compute Instance, choosing its name and its sizing:
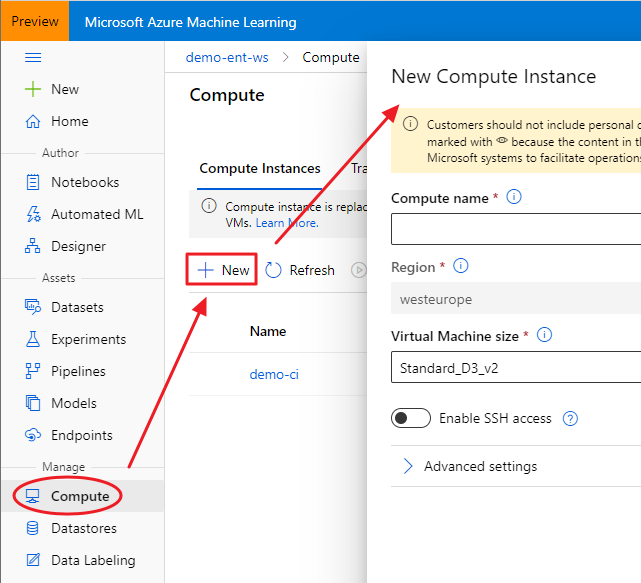
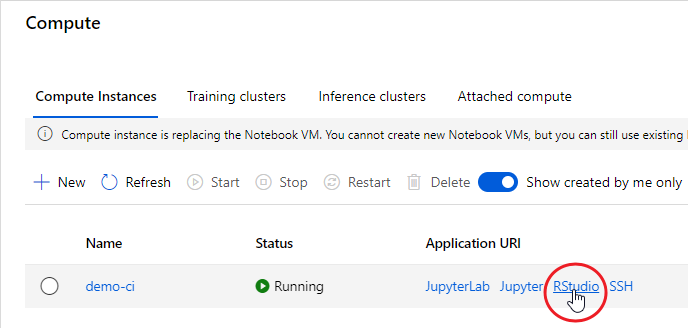
The advantage of using a Compute Instance is that the most used software and libraries by data scientists are already installed, including the Azure ML Python SDK and RStudio Server Open Source Edition. That said, once your Compute Instance is started, you can connect to RStudio using the proper link:
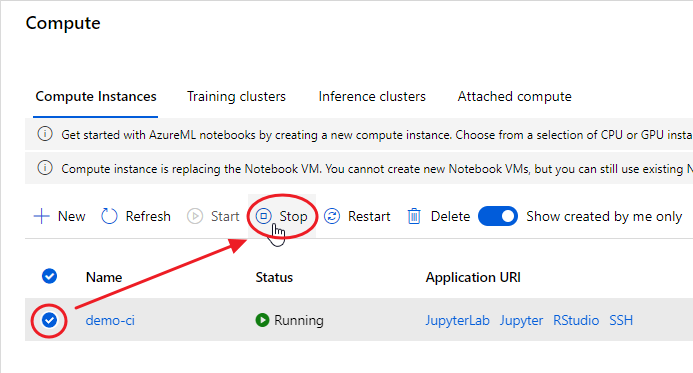
At the end of your experimentation, remember to shut down your Compute Instance, otherwise you’ll be charged according to the chosen plan:
Set Up Your Machine From Scratch
First of all you need to install the R engine from CRAN or MRAN. Then you could also install RStudio Desktop, the preferred IDE of R professionals.
The next step is to install Conda, because the R SDK needs to bind to the Python SDK through reticulate. If you really don’t need Anaconda for specific purposes, it’s recommended to install a lightweight version of it, Miniconda. During its installation, let the installer add the conda installation of Python to your PATH environment variable.
Install The R SDK
Open your RStudio, simply create a new R script (File → New File → R Script) and install the last stable version of Azure ML R SDK package (azuremlsdk) available on CRAN in the following way:install.packages("remotes")
remotes::install_cran("azuremlsdk")
If you want to install the latest committed version of the package from GitHub (maybe because the product team has fixed an annoying bug), you can instead use the following function:
remotes::install_github('https://github.com/Azure/azureml-sdk-for-r')
During the installation you could get this error:

In this case, you just need to set the TZ environment variable with your preferred timezone:
Sys.setenv(TZ="GMT")
Then simply re-install the R SDK.
You may also be asked to update some dependent packages:
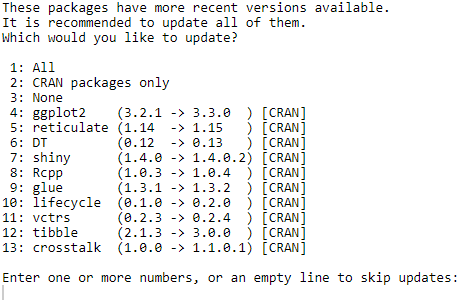
If you don’t have any requirement about dependencies in your project, it’s always better to update them all (put focus on the prompt in the console; press 1; press enter).
If you are on your Compute Instance and you get a warning like the following one:

just put the focus on the console and press “n”, since the Compute Instance environment already has a Conda installation. Microsoft engineers are already investigating on this issue.
You need then to install the Azure ML Python SDK, otherwise your azuremlsdk R package won’t work. You can do that directly from RStudio thanks to an azuremlsdk function:
azuremlsdk::install_azureml(remove_existing_env = TRUE)
The remove_existing_env parameter set to TRUE will remove the default Azure ML SDK environment r-reticulate if previously installed (it’s a way to clean up a Python SDK installation).
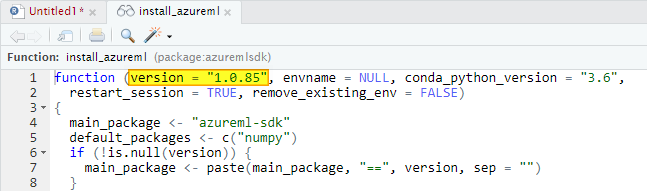
Just keep in mind that in this way you’ll install the version of the Azure ML Python SDK expected by your installed version of the azuremlsdk package. You can check what version you will install putting the cursor over the install_azureml function and visualizing the code definition clicking F2:
Sometimes there are new feature and fixes on the latest version of the Python SDK. If you need to install it, first check what version is available on this link:
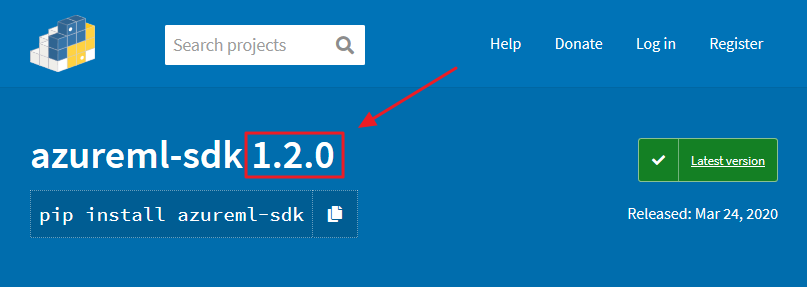
Then use that version number in the following code:
azuremlsdk::install_azureml(version = "1.2.0", remove_existing_env = TRUE)
Sometimes you may need to install an updated version of a single component of the Azure ML Python SDK to test, for example new features. Supposing you want to update the Azure ML Data Prep SDK, here the code you could use:
reticulate::py_install("azureml-dataprep==1.4.2", envname = "r-reticulate", pip = TRUE)
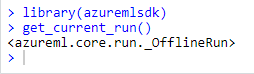
In order to check if the installation is working correctly, try this:
library(azuremlsdk) get_current_run()
It should return something like this:
Great! You’re now ready to spin the Azure ML wheels using your preferred programming language: R!
Conclusions
After a long period during which Microsoft focused exclusively on Python SDK to enable data scientists to benefit from Azure computing and storage services, they recently released the R SDK too. This article focuses on the steps needed to install the Azure Machine Learning R SDK on your preferred environment.
Next articles will deal with the R SDK main capabilities.


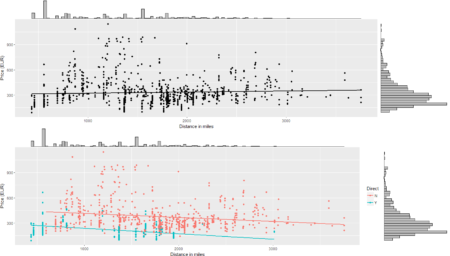 To conclude the 4-step (flight) trip from data acquisition to data analysis, let's recap the most important concepts described in each of the post:
1)
To conclude the 4-step (flight) trip from data acquisition to data analysis, let's recap the most important concepts described in each of the post:
1) 
 The collection of example flight data in json format available in
The collection of example flight data in json format available in 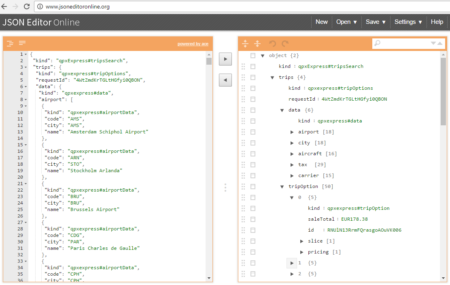 However, looking deeply into the object, several other elements are provided as the distance in mile, the segment, the duration, the carrier, etc. The R parser to transform the json structure in a usable dataframe requires the dplyr library for using the pipe operator (%>%) to streamline the code and make the parser more readable. Nevertheless, the library actually wrangling through the lines is tidyjson and its powerful functions:
However, looking deeply into the object, several other elements are provided as the distance in mile, the segment, the duration, the carrier, etc. The R parser to transform the json structure in a usable dataframe requires the dplyr library for using the pipe operator (%>%) to streamline the code and make the parser more readable. Nevertheless, the library actually wrangling through the lines is tidyjson and its powerful functions: