Outliers and Domain Knowledge
I would like to share some thoughts about outliers and domain knowledge.
One of the common steps during the data exploration stage is the search for outliers. Some analysis methods such as regression are very sensitive to outliers. As an example of sensitivity, in the following data (10,10) is an outlier. Including the outlier produces a regression line y = .26 + .91x, while excluding the outlier produces the very different regression line y = 2.
x <- c(1,1,1,2,2,2,3,3,3,10)
y <- c(1,2,3,1,2,3,1,2,3,10)
df <- data.frame(cbind(x,y))
lm(y ~ x, df)
plot(x,y, pch=16)
abline(lm(y ~ x, df)
Statistics books sometimes define an outlier as being outside the range of Q1 ± 1.5IQR or Q1 ± 3IQR, where Q1 is the lower quartile (25th percentile value), Q3 is the upper quartile (75th percentile value), and the interquartle range IQR = Q3 – Q1.
What does one do with an outlier? It could be bad data. It is pretty unlikely that there is a graduate student who is age 9, but we don’t know whether the value should be 19 (very rare, but possible), or 29 (likely), or 39 or more (not so rare). If we have the opportunity to ask the owner of the data, perhaps we can get the value corrected. More likely is we can not ask the owner. We can delete the entire observation, or we can pretend to correct the value with a mode or median value or a judgmental value.
Perhaps the outlier is not bad data but rather just an unusual value. In a portfolio of property or liability insurance claims, the distribution is often positively skewed (mean greater than mode, a long tail to the positive side of the mode). Most claims are small, but occasionally there is that one enormous claim. What does one do with that outlier value? Some authors consider data science to be the Venn diagram intersection among math/statistics, computer science, and domain knowledge (see for example Drew Conway, in drewconway.com/zia/2013/3/26/the-data-science-venn-diagram). If the data scientist is not the domain expert, he or she should consult with one. With insurance claims there are several possibilities. One is that the enormous claim is one that is unlikely to reoccur for any number of reasons. Hopefully there will never be another September 11 type destruction of two World Trade Center buildings owned by a single owner. Another example is when the insurance policy terms are revised to literally prohibit a specific kind of claim in the future. Another possibility is that the specific claim is unlikely to reoccur (the insurance company stopped insuring wheelchairs, so there won’t be another wheelchair claim), but that claim is representative of another kind of claim that is likely to occur. In this case, the outlier should not be deleted. One author has said it takes Solomon-like wisdom to discern which possibility to believe.
An interesting example of outliers occurs with sports data. For many reasons, US major league baseball player statistics have changed over the years. There are more great home run seasons nowadays than decades ago, but there are fewer great batting average seasons. Baseball fanatics know the last .400 hitter (40% ratio of hits divided by at bats over the entire season) was Ted Williams in 1941. If we have 80 years of baseball data and we are predicting the probability of another .400 hitter, we would predict close to zero. It’s possible, but extremely unlikely, right? Actually no. Assuming there will still be a shortened season in 2020, a decision that may change, this author is willing to forecast that there will be a .400 hitter in a shortened season. This is due to the theory that batters need less time in spring training practice to be at full ability than pitchers, and it is easier to achieve .400 in a small number of at bats earlier in the season when the pitchers are not at full ability. This is another example of domain expertise as a lifetime baseball fan.

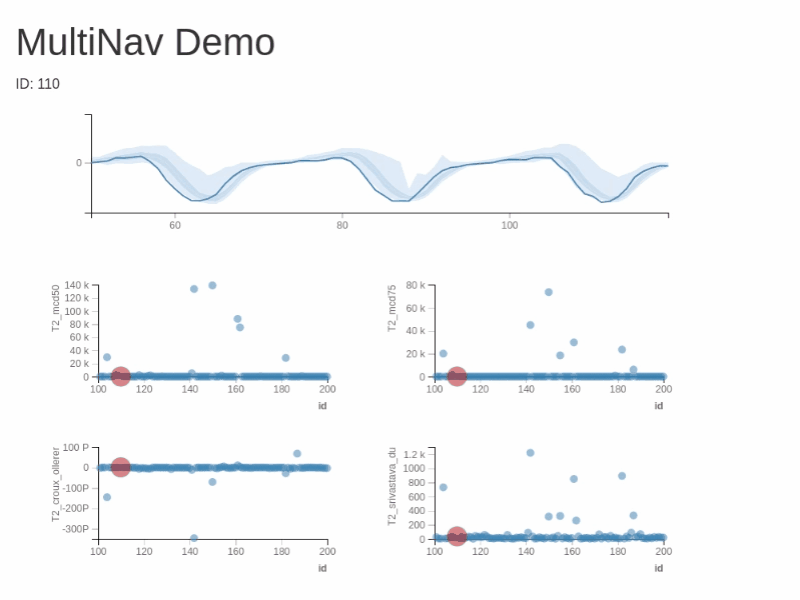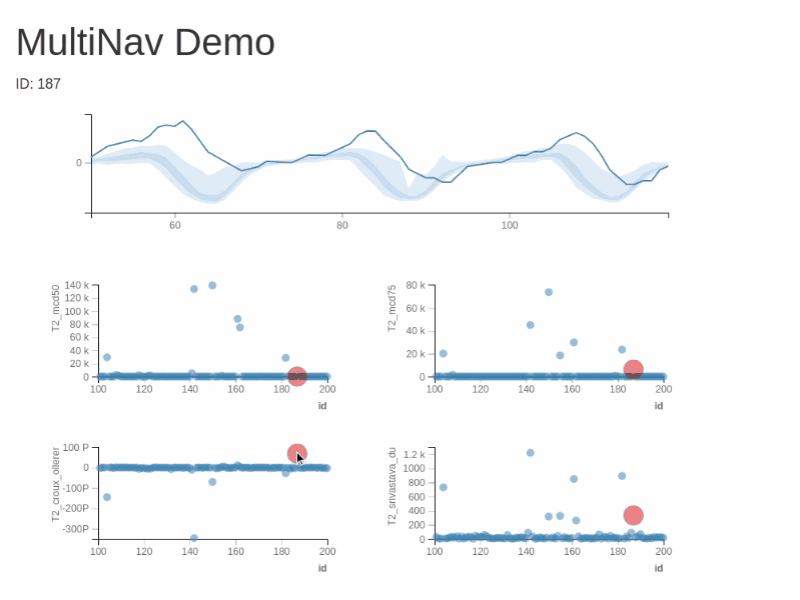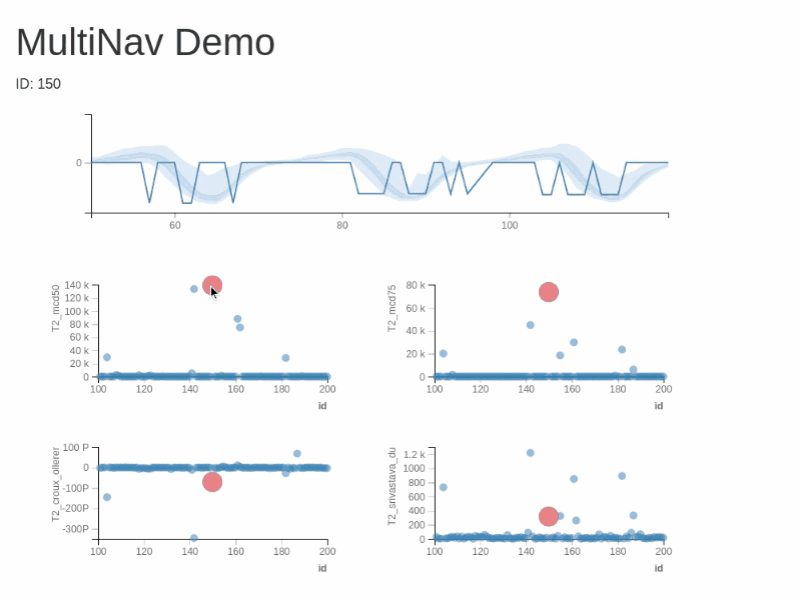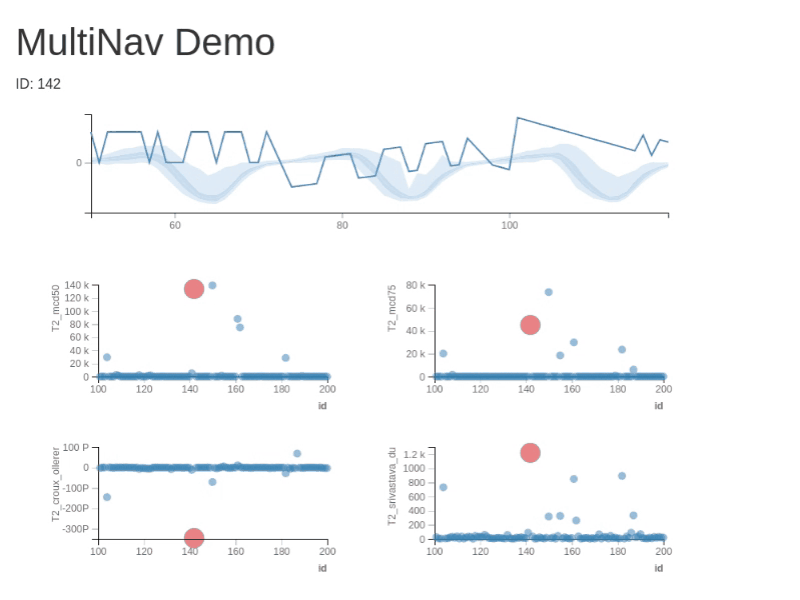
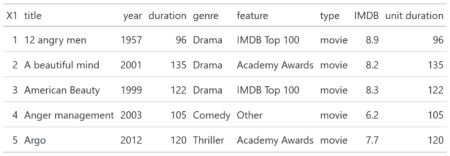
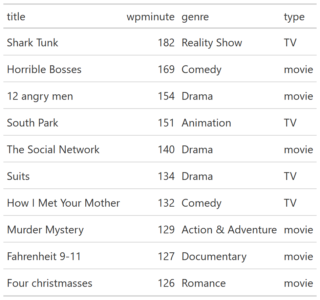



 You can test RXSpreadsheet by installing the GitHub version with devtools::install_github(‘MichaelHogers/RXSpreadsheet’) and subsequently running RXSpreadsheet::runExample().
This wrapper was made by Jiawei Xu and Michael Hogers. We are aiming for a CRAN release over the coming weeks. Special thanks to NPL Markets for encouraging us to release open source software.
You can test RXSpreadsheet by installing the GitHub version with devtools::install_github(‘MichaelHogers/RXSpreadsheet’) and subsequently running RXSpreadsheet::runExample().
This wrapper was made by Jiawei Xu and Michael Hogers. We are aiming for a CRAN release over the coming weeks. Special thanks to NPL Markets for encouraging us to release open source software. 

 [contact-form][contact-field label=”Name” type=”name” required=”true” /][contact-field label=”Email” type=”email” required=”true” /][contact-field label=”Website” type=”url” /][contact-field label=”Message” type=”textarea” /][/contact-form]
[contact-form][contact-field label=”Name” type=”name” required=”true” /][contact-field label=”Email” type=”email” required=”true” /][contact-field label=”Website” type=”url” /][contact-field label=”Message” type=”textarea” /][/contact-form]