Here is an open source desktop text editor that integrates both externally defined variable definitions and R. In the following demo video, R is used shortly after the 5-minute mark:
Thoughts on the concept of integrated variables?
Download: https://github.com/DaveJarvis/scrivenvar/blob/master/README.md#download
Stay safe everyone.
Category: R
ROC for Decision Trees – where did the data come from?
ROC for Decision Trees – where did the data come from?
By Jerry Tuttle
In doing decision tree classification problems, I have often graphed the ROC (Receiver Operating Characteristic) curve. The True Positive Rate (TPR) is on the y-axis, and the False Positive Rate (FPR) is on the x-axis. True Positive is when the lab test predicts you have the disease and you actually do have it. False Positive is when the lab test predicts you have the disease but you actually do not have it.
The following code uses the sample dataset kyphosis from the rpart package, creates a default decision tree, prints the confusion matrix, and plots the ROC curve. (Kyphosis is a type of spinal deformity.)
library(rpart)
df <- kyphosis
set.seed(1)
mytree <- rpart(Kyphosis ~ Age + Number + Start, data = df, method="class")
library(rattle)
library(rpart.plot)
library(RColorBrewer)
fancyRpartPlot(mytree, uniform=TRUE, main="Kyphosis Tree")
predicted <- predict(mytree, type="class")
table(df$Kyphosis,predicted)
library(ROCR)
pred <- prediction(predict(mytree, type="prob")[, 2], df$Kyphosis)
plot(performance(pred, "tpr", "fpr"), col="blue", main="ROC Kyphosis, using library ROCR")
abline(0, 1, lty=2)
auc <- performance(pred, "auc")
[email protected]
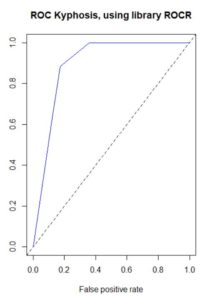
However, for a long time there has been a disconnect in my mind between the confusion matrix and the ROC curve. The confusion matrix provides a single value of the ordered pair (x=FPR, y=TPR) on the ROC curve, but the ROC curve has a range of values. Where are the other values coming from?
The answer is that a default decision tree confusion matrix uses a single probability threshold value of 50%. A decision tree ends in a set of terminal nodes. Every observation falls in exactly one of those terminal nodes. The predicted classification for the entire node is based on whichever classification has the greater percentage of observations, which for binary classifications requires a probability greater than 50%. So for example if a single observation has predicted probability based on its terminal node of 58% that the disease is present, then a 50% threshold would classify this observation as disease being present. But if the threshold were changed to 60%, then the observation would be classified as disease not being present.
The ROC curve uses a variety of probability thresholds, reclassifies each observation, recalculates the confusion matrix, and recalculates a new value of the ordered pair (x=FPR, y=TPR) for the ROC curve. The resulting curve shows the spread of these ordered pairs over all (including interpolated, and possibly extrapolated) probability thresholds, but the threshold values are not commonly displayed on the curve. Plotting performance in the ROCR package does this behind the scenes, but I wanted to verify this myself. This dataset has a small number of predictions of disease present, and at large threshold values the prediction is zero, resulting in a one column confusion matrix and zero FPR and TPR. The following code individually applies different probability thresholds to build the ROC curve, although it does not extrapolate for large values of FPR and TPR.
dat <- data.frame()
s <- predict(mytree, type="prob")[, 2]
for (i in 1:21){
p <- .05*(i-1)
thresh p, “present”, “absent”)
t <- table(df$Kyphosis,thresh)
fpr <- ifelse(ncol(t)==1, 0, t[1,2] / (t[1,2] + t[1,1]))
tpr <- ifelse(ncol(t)==1, 0, t[2,2] / (t[2,2] + t[2,1]))
dat[i,1] <- fpr
dat[i,2] <- tpr
}
colnames(dat) <- c("fpr", "tpr")
plot(x=dat$fpr, y=dat$tpr, xlab="FPR", ylab="TPR", xlim=c(0,1), ylim=c(0,1),
main="ROC Kyphosis, using indiv threshold calcs", type="b", col="blue")
abline(0, 1, lty=2)
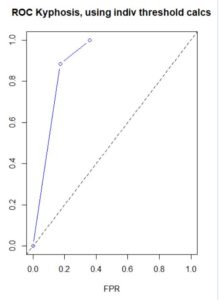
By Jerry Tuttle
In doing decision tree classification problems, I have often graphed the ROC (Receiver Operating Characteristic) curve. The True Positive Rate (TPR) is on the y-axis, and the False Positive Rate (FPR) is on the x-axis. True Positive is when the lab test predicts you have the disease and you actually do have it. False Positive is when the lab test predicts you have the disease but you actually do not have it.
The following code uses the sample dataset kyphosis from the rpart package, creates a default decision tree, prints the confusion matrix, and plots the ROC curve. (Kyphosis is a type of spinal deformity.)
library(rpart)
df <- kyphosis
set.seed(1)
mytree <- rpart(Kyphosis ~ Age + Number + Start, data = df, method="class")
library(rattle)
library(rpart.plot)
library(RColorBrewer)
fancyRpartPlot(mytree, uniform=TRUE, main="Kyphosis Tree")
predicted <- predict(mytree, type="class")
table(df$Kyphosis,predicted)
library(ROCR)
pred <- prediction(predict(mytree, type="prob")[, 2], df$Kyphosis)
plot(performance(pred, "tpr", "fpr"), col="blue", main="ROC Kyphosis, using library ROCR")
abline(0, 1, lty=2)
auc <- performance(pred, "auc")
[email protected]

However, for a long time there has been a disconnect in my mind between the confusion matrix and the ROC curve. The confusion matrix provides a single value of the ordered pair (x=FPR, y=TPR) on the ROC curve, but the ROC curve has a range of values. Where are the other values coming from?
The answer is that a default decision tree confusion matrix uses a single probability threshold value of 50%. A decision tree ends in a set of terminal nodes. Every observation falls in exactly one of those terminal nodes. The predicted classification for the entire node is based on whichever classification has the greater percentage of observations, which for binary classifications requires a probability greater than 50%. So for example if a single observation has predicted probability based on its terminal node of 58% that the disease is present, then a 50% threshold would classify this observation as disease being present. But if the threshold were changed to 60%, then the observation would be classified as disease not being present.
The ROC curve uses a variety of probability thresholds, reclassifies each observation, recalculates the confusion matrix, and recalculates a new value of the ordered pair (x=FPR, y=TPR) for the ROC curve. The resulting curve shows the spread of these ordered pairs over all (including interpolated, and possibly extrapolated) probability thresholds, but the threshold values are not commonly displayed on the curve. Plotting performance in the ROCR package does this behind the scenes, but I wanted to verify this myself. This dataset has a small number of predictions of disease present, and at large threshold values the prediction is zero, resulting in a one column confusion matrix and zero FPR and TPR. The following code individually applies different probability thresholds to build the ROC curve, although it does not extrapolate for large values of FPR and TPR.
dat <- data.frame()
s <- predict(mytree, type="prob")[, 2]
for (i in 1:21){
p <- .05*(i-1)
thresh p, “present”, “absent”)
t <- table(df$Kyphosis,thresh)
fpr <- ifelse(ncol(t)==1, 0, t[1,2] / (t[1,2] + t[1,1]))
tpr <- ifelse(ncol(t)==1, 0, t[2,2] / (t[2,2] + t[2,1]))
dat[i,1] <- fpr
dat[i,2] <- tpr
}
colnames(dat) <- c("fpr", "tpr")
plot(x=dat$fpr, y=dat$tpr, xlab="FPR", ylab="TPR", xlim=c(0,1), ylim=c(0,1),
main="ROC Kyphosis, using indiv threshold calcs", type="b", col="blue")
abline(0, 1, lty=2)

R can help decide the opening of pandemic-ravaged economies
Epidemiological models do not provide death forecasts. Statistical models using inverse Mills ratio, generalized linear models (GLM) with Poisson link for death count data plus autoregressive distributed lag (ARDL) models can provide improved death forecasts for individual states.
See details at http://ssrn.com/abstract=3637682 and http://ssrn.com/abstract=3649680
Our 95% confidence interval is [optimistic 4719 to pessimistic 8026] deaths, with a point-estimate forecast for US deaths at 6529 for the week ending July 27, 2020.
Following 2 functions may be useful. We are finding 95%
confidence intervals for the individual state forecast of the last count of Covid-19 deaths using my `meboot’ package. I recommend using reps=1000 for more reliable confidence intervals.
fittedLast=function(yt,zt){
#ARDL(1,1) says yt=a+b1 zt =b2 yLag +b3 zLag + err
yt= actual NEW deaths on week t or ND
zt= NEW deaths forecast by US wide model using IMR or PredNewDeaths
#we expect one less weeks of data for predicted new deaths or zt
yt=as.numeric(yt)
zt=as.numeric(zt)
nweeks=length(yt)
if (length(zt)!=nweeks) stop(“unmatched yt zt in fittedLast”)
yt is nweeks X 1 vector# zt is for (nweek-1) X 1 vector
yLag=as.numeric(yt[1:(nweeks-1)])
yyt=as.numeric(yt[2:nweeks])
zzt=as.numeric(zt[2:nweeks])
zLag=as.numeric(zt[1:(nweeks-1)])
not sure if glm will work
latest.fitted=NA
if(min(yt)>0 & min(zt)>0){
reg=glm(yyt~yLag+zzt+zLag,family=poisson(link = “log”))
#reg=lm(yyt~yLag+zzt)
f1=fitted.values(reg)
#f1=fitted(reg)
latest.fitted=f1[length(f1)]
}
return(latest.fitted)
}#end function fittedLast
#example
#set.seed(99)
#z=sample(1:10);y=sample(1:11);
#fittedLast(y,z)
#reg=lm(y[2:10]~y[1:9]+z[2:10])
#print(cbind(y[2:10],fitted(reg)))
#coef(reg)
ARDL95=function(yt,zt,reps=100){
require(meboot)
yt= actual NEW deaths on week t or ND
zt= NEW deaths forecast by US wide model using IMR or PredNewDeaths
#we expect equal no of weeks of data for predicted new deaths or zt
#calls fittedLast which fits
#ARDL(1,1) says yt=a+b1 zt =b2 yLag +b3 zLag + err
yt=as.numeric(yt)
zt=round(as.numeric(zt),0)
nweeks=length(yt)
if (length(zt)!=(nweeks)) stop(“unmatched yt zt in fittedLast”)
mid=fittedLast(yt=yt, zt=zt) #middle of confInterval
#create data
y.ens=meboot(x=as.numeric(yt), reps=reps)$ens
z.ens=meboot(x=as.numeric(zt), reps=reps)$ens
outf=rep(NA,nweeks)#place to store
for (j in 1:reps){
outf[j]=fittedLast(yt=y.ens[,j],z.ens[,j])
}# end j loop over reps
#use ensembles above to get 95percent conf interval
#of the latest.fitted
qu1=quantile(outf,prob=c(0.025,0.975),na.rm=TRUE)
out3=c(qu1[1],mid,qu1[2])
return(out3)
}#end function ARDL95
Following 2 functions may be useful. We are finding 95%
confidence intervals for the individual state forecast of the last count of Covid-19 deaths using my `meboot’ package. I recommend using reps=1000 for more reliable confidence intervals.
fittedLast=function(yt,zt){
#ARDL(1,1) says yt=a+b1 zt =b2 yLag +b3 zLag + err
yt= actual NEW deaths on week t or ND
zt= NEW deaths forecast by US wide model using IMR or PredNewDeaths
#we expect one less weeks of data for predicted new deaths or ztyt=as.numeric(yt)
zt=as.numeric(zt)
nweeks=length(yt)
if (length(zt)!=nweeks) stop(“unmatched yt zt in fittedLast”)
yt is nweeks X 1 vector# zt is for (nweek-1) X 1 vector
yLag=as.numeric(yt[1:(nweeks-1)])yyt=as.numeric(yt[2:nweeks])
zzt=as.numeric(zt[2:nweeks])
zLag=as.numeric(zt[1:(nweeks-1)])
not sure if glm will work
latest.fitted=NAif(min(yt)>0 & min(zt)>0){
reg=glm(yyt~yLag+zzt+zLag,family=poisson(link = “log”))
#reg=lm(yyt~yLag+zzt)
f1=fitted.values(reg)
#f1=fitted(reg)
latest.fitted=f1[length(f1)]
}
return(latest.fitted)
}#end function fittedLast
#example
#set.seed(99)
#z=sample(1:10);y=sample(1:11);
#fittedLast(y,z)
#reg=lm(y[2:10]~y[1:9]+z[2:10])
#print(cbind(y[2:10],fitted(reg)))
#coef(reg)
ARDL95=function(yt,zt,reps=100){
require(meboot)
yt= actual NEW deaths on week t or ND
zt= NEW deaths forecast by US wide model using IMR or PredNewDeaths
#we expect equal no of weeks of data for predicted new deaths or zt#calls fittedLast which fits
#ARDL(1,1) says yt=a+b1 zt =b2 yLag +b3 zLag + err
yt=as.numeric(yt)
zt=round(as.numeric(zt),0)
nweeks=length(yt)
if (length(zt)!=(nweeks)) stop(“unmatched yt zt in fittedLast”)
mid=fittedLast(yt=yt, zt=zt) #middle of confInterval
#create data
y.ens=meboot(x=as.numeric(yt), reps=reps)$ens
z.ens=meboot(x=as.numeric(zt), reps=reps)$ens
outf=rep(NA,nweeks)#place to store
for (j in 1:reps){
outf[j]=fittedLast(yt=y.ens[,j],z.ens[,j])
}# end j loop over reps
#use ensembles above to get 95percent conf interval
#of the latest.fitted
qu1=quantile(outf,prob=c(0.025,0.975),na.rm=TRUE)
out3=c(qu1[1],mid,qu1[2])
return(out3)
}#end function ARDL95
labourR 1.0.0: Automatic Coding of Occupation Titles
Occupations classification is an important step in tasks such as labour market analysis, epidemiological studies and official statistics. To assist research on the labour market, ESCO has defined a taxonomy for occupations. Occupations are specified and organized in a hierarchical structure based on the International Standard Classification of Occupations (ISCO).
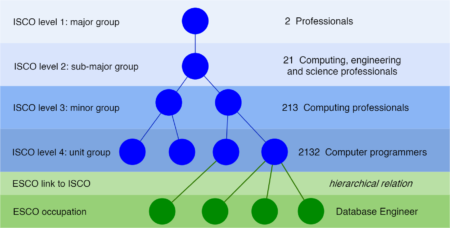
The initial motivation was to retrieve the work experience history from a Curriculum Vitae generated from the Europass online CV editor. Document vectorization is performed using the ESCO model and a fuzzy match is allowed with various string distance metrics.
The
Example
Given an ISCO level, the top suggested ISCO group is returned.
labourR is a new package that performs occupations coding for multilingual free-form text (e.g. a job title) using the ESCO hierarchical classification model.
The initial motivation was to retrieve the work experience history from a Curriculum Vitae generated from the Europass online CV editor. Document vectorization is performed using the ESCO model and a fuzzy match is allowed with various string distance metrics.
The
labourR package:- Allows classifying multilingual free-text using the ESCO-ISCO hierarchy of occupations.
- Computations are fully vectorized and memory efficient.
- Includes facilities to assist research in information mining of labour market data.
Installation
You can install the released version of labourR from CRAN with,install.packages("labourR")
library(labourR) corpus <- data.frame( id = 1:3, text = c("Data Scientist", "Junior Architect Engineer", "Cashier at McDonald's") )
num_leaves specifies the number of ESCO occupations used to perform a plurality vote,classify_occupation(corpus = corpus, isco_level = 3, lang = "en", num_leaves = 5) #> id iscoGroup preferredLabel #> 1: 1 251 Software and applications developers and analysts #> 2: 2 214 Engineering professionals (excluding electrotechnology) #> 3: 3 523 Cashiers and ticket clerksFor further information browse the vignettes.
Preview data with either head or heaD
R is a case sensitive programming language, which sometimes creates unusual and yet annoying problems for users. A common mistake that I often make when using R is to press the shift button too early when I use the
To create a new
head() function – which results in heaD(). However, this returns an error message (not surprisingly) rather than printing the first six rows of the data.
> head(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
> heaD(mtcars)
Error in heaD(mtcars) : could not find function "heaD"
At the beginning, this didn’t bother me since I could easily fix this typo but over time it has become a bit annoying. The faster I typed in R, the more I repeated this mistake. Then I thought creating a heaD() function that does the same job as head() would be the ultimate solution to my problem. Because I would need this “new” function every time I open R, I decided to add it into my .Rprofile file. The .Rprofile file contains R code to be run when R starts up. Typically .Rprofile is located in the user’s home directory. In my computer, I place it under: C:\Users\okanb\OneDrive\DocumentsTo create a new
.Rprofile file, you can simply create a text file using a text editor, add the content to be used when R starts up, and save it as .Rprofile (i.e., no file name and the file extension is .Rprofile). If you already have this file in your computer, you can simply run usethis::edit_r_profile() to open and edit the file in R. In the file, I added the following line: # Create a heaD function
heaD <- function(x) head(x) # or just: heaD <- head
After editing and saving .Rprofile, you need to restart R. From this point on, R will recognize both head() and heaD().> heaD(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
Creating custom neural networks with nnlib2Rcpp
For anyone interested, this is a post about creating arbitrary, new, or custom Neural Networks (NN) using the nnlib2Rcpp R package. The package provides some useful NN models that are ready to use. Furthermore, it can be a versatile basis for experimentation with new or custom NN models, which is what this brief tutorial is about. A warning is necessary at this point:
Warning: the following text contains traces of C++ code. If you are in any way sensitive to consuming C++, please abandon reading immediately.
The NN models in nnlib2Rcpp are created using a collection of C++ classes written for creating NN models called nnlib2. A cut-down class-diagram of the classes (and class-templates) in this collection can be found here . The most important class in the collection is “component” (for all components that constitute a NN). Objects of class “component” can be added to a NN “topology” (hosted in objects of class “nn”) and interact with each other. Layers of processing nodes (class “layer”), groups of connections (class “connection_set”), and even entire neural nets (class “nn”) are based on class “component”. When implementing new components, it is also good to remember that:
– Objects of class “layer” contain objects of class “pe” (processing elements [or nodes]).
– Template “Layer” simplifies creation of homogeneous “layer” sub-classes containing a particular “pe” subclass (i.e. type of nodes).
– Objects of class “connection_set” contain objects of class “connection”.
– Template “Connection_Set” simplifies creation of homogeneous “connection_set” sub-classes containing a particular “connection” subclass (i.e. type of connections).
– Customized and modified NN components and sub-components are to be defined based on these classes and templates.
– All aforementioned classes have an “encode” (training) and a “recall” (mapping) method; both are virtual and can be overridden with custom behavior. Calling “nn” “encode” triggers the “encode” function of all the components in its topology which, in turn, triggers “encode” for “pe” objects (processing nodes) in a “layer” or “connection” objects in a “connection_set”. Similarly for “recall”.
The NN to create in this example will be based on Perceptron, the most classic of them all. It is not yet implemented in nnlib2Rcpp, so in this example we will play the role of Prof. Rosenblatt and his team [6] and implement a simple multi-class Perceptron ourselves. Unlike, Prof Rosenblatt, you -instead of inventing it- can find information about it in a wikipedia page for it [1]. We will implement a simplified (not 100% scientifically sound) variation, with no bias, fixed learning rate (at 0.3) and connection weights initialized to 0.
Let’s add it to nnlib2Rcpp.
Step 1: setup the tools needed.
To follow this example, you will need to have Rtools [2] and the Rcpp R package [3] installed, and the nnlib2Rcpp package source (version 0.1.4 or above). This can be downloaded from CRAN [4] or the latest version can be found on github [5]. If fetched or downloaded from github, the nnlib2Rcpp.Rproj is a project file for building the package in RStudio. I recommend getting the source from github, unpacking it (if needed) in a directory and then opening the aforementioned nnlib2Rcpp.Rproj in Rstudio. You can then test-build the unmodified package; if it succeeds you can proceed to the next step, adding your own NN components.
Step 2: define the model-specific components and sub-components.
Open the “additional_parts.h” C++ header file found in sub-directory “src” and create the needed classes. Much of the default class behavior is similar to what is required for a Perceptron, so we will focus on what is different and specific to the model. We will need to define (in the “additional_parts.h” file) the following:
(a) a “pe” subclass for the Perceptron processing nodes. All “pe” objects provide three methods, namely “input_function”, “activation_function”, and “threshold_function”; by default, each is applied to the result of the previous one, except for the “input_function” which gathers (by default sums) all incoming values and places result on the internal register variable “input”. The sequence of executing these methods is expected to place the final result in “pe” variable “output”. You may choose (or choose not) to modify these methods if this fits your model and implementation approach. You may also choose to modify “pe” behavior in its “encode” and/or “recall” functions, possibly bypassing the aforementioned methods completely. It may help to see the “pe.h” header file (also in directory “src”) for more insight on the base class. In any case, a C++ implementation for Perceptron processing nodes could be:
Note: for compatibility with nnlib2Rcpp version 0.1.4 (the current version on CRAN)- the example above assumes that the desired values are placed as input to the processing nodes right before update of weights (encoding); version 0.1.5 and above provides direct access from R to the “misc” variables that nodes and connections maintain (via “NN” method “set_misc_values_at”, more on “NN” below). It may have been more elegant to use these “misc” variables for holding desired output in processing nodes instead of “input”.
(d) Next, you may want to define a class for groups of such connections, which can be done quickly using the template “Connection_Set”:
Again in the “additional_parts.h” C++ header file found in directory “src” add code that creates Percepron layers and groups of connections when a particular name is used. Locate the “generate_custom_layer” function and add to it the line:
Note: as of July 15, 2020 all the aforementioned changes to “additional_parts.h” C++ header are already implemented as an example in the nnlib2Rcpp version 0.1.5 github repo [5].
That is it. You can now build the modified library and then return to the R world to use your newly created Perceptron components in a NN. The “NN” R module in nnlib2Rcpp allows you to combine these (and other) components in a network and then use it in R.
It is now time to see if this cut-down modified Perceptron is any good. In the example below, the iris dataset is used to train it. The example uses the “NN” R module in nnlib2Rcpp to build the network and then trains and tests it. The network topology consists of a generic input layer (component #1) of size 4 i.e. as many nodes as the iris features, a set of connections (component #2) whose weights are initialized to 0 (in create_connections_in_sets) below, and a processing layer (component #3) of size 3 i.e. as many nodes as the iris species:
iris case 1 , desired = 1 0 0 returned = 1 0 0
iris case 2 , desired = 1 0 0 returned = 1 0 0
iris case 3 , desired = 1 0 0 returned = 1 0 0
…
iris case 148 , desired = 0 0 1 returned = 0 0 1
iris case 149 , desired = 0 0 1 returned = 0 0 1
iris case 150 , desired = 0 0 1 returned = 0 0 1
Anyway, this example was not about classification success but about creating a new NN type in the nnlib2Rcpp R package. I hope it will be useful to some of you out there.
Links (all accessed July 12, 2020):
[1] Perceptron:
https://en.wikipedia.org/w/index.php?title=Perceptron&oldid=961536136
[2] RTools:
https://cran.r-project.org/bin/windows/Rtools/history.html
[3] Rcpp package:
https://cran.r-project.org/web/packages/Rcpp/index.html
[4] nnlib2Rcpp package on CRAN:
https://cran.r-project.org/web/packages/nnlib2Rcpp/index.html
[5] nnlib2Rcpp package on github:
https://github.com/VNNikolaidis/nnlib2Rcpp
[6] Frank Rosenblatt:
https://en.wikipedia.org/wiki/Frank_Rosenblatt
PS. Time permitting, more components will be added to the collection (and added to nnlib2Rcpp), maybe accompanied by posts similar to this one; these will eventually be available in the package. Any interesting or useful NN component that you would like to contribute is welcomed (credit, of course, will go to you, its creator); if so, please contact me using the comments below. (Another project is to create parallel-processing versions of the components, if anyone wants to help).
Warning: the following text contains traces of C++ code. If you are in any way sensitive to consuming C++, please abandon reading immediately.
The NN models in nnlib2Rcpp are created using a collection of C++ classes written for creating NN models called nnlib2. A cut-down class-diagram of the classes (and class-templates) in this collection can be found here . The most important class in the collection is “component” (for all components that constitute a NN). Objects of class “component” can be added to a NN “topology” (hosted in objects of class “nn”) and interact with each other. Layers of processing nodes (class “layer”), groups of connections (class “connection_set”), and even entire neural nets (class “nn”) are based on class “component”. When implementing new components, it is also good to remember that:
– Objects of class “layer” contain objects of class “pe” (processing elements [or nodes]).
– Template “Layer” simplifies creation of homogeneous “layer” sub-classes containing a particular “pe” subclass (i.e. type of nodes).
– Objects of class “connection_set” contain objects of class “connection”.
– Template “Connection_Set” simplifies creation of homogeneous “connection_set” sub-classes containing a particular “connection” subclass (i.e. type of connections).
– Customized and modified NN components and sub-components are to be defined based on these classes and templates.
– All aforementioned classes have an “encode” (training) and a “recall” (mapping) method; both are virtual and can be overridden with custom behavior. Calling “nn” “encode” triggers the “encode” function of all the components in its topology which, in turn, triggers “encode” for “pe” objects (processing nodes) in a “layer” or “connection” objects in a “connection_set”. Similarly for “recall”.
The NN to create in this example will be based on Perceptron, the most classic of them all. It is not yet implemented in nnlib2Rcpp, so in this example we will play the role of Prof. Rosenblatt and his team [6] and implement a simple multi-class Perceptron ourselves. Unlike, Prof Rosenblatt, you -instead of inventing it- can find information about it in a wikipedia page for it [1]. We will implement a simplified (not 100% scientifically sound) variation, with no bias, fixed learning rate (at 0.3) and connection weights initialized to 0.
Let’s add it to nnlib2Rcpp.
Step 1: setup the tools needed.
To follow this example, you will need to have Rtools [2] and the Rcpp R package [3] installed, and the nnlib2Rcpp package source (version 0.1.4 or above). This can be downloaded from CRAN [4] or the latest version can be found on github [5]. If fetched or downloaded from github, the nnlib2Rcpp.Rproj is a project file for building the package in RStudio. I recommend getting the source from github, unpacking it (if needed) in a directory and then opening the aforementioned nnlib2Rcpp.Rproj in Rstudio. You can then test-build the unmodified package; if it succeeds you can proceed to the next step, adding your own NN components.
Step 2: define the model-specific components and sub-components.
Open the “additional_parts.h” C++ header file found in sub-directory “src” and create the needed classes. Much of the default class behavior is similar to what is required for a Perceptron, so we will focus on what is different and specific to the model. We will need to define (in the “additional_parts.h” file) the following:
(a) a “pe” subclass for the Perceptron processing nodes. All “pe” objects provide three methods, namely “input_function”, “activation_function”, and “threshold_function”; by default, each is applied to the result of the previous one, except for the “input_function” which gathers (by default sums) all incoming values and places result on the internal register variable “input”. The sequence of executing these methods is expected to place the final result in “pe” variable “output”. You may choose (or choose not) to modify these methods if this fits your model and implementation approach. You may also choose to modify “pe” behavior in its “encode” and/or “recall” functions, possibly bypassing the aforementioned methods completely. It may help to see the “pe.h” header file (also in directory “src”) for more insight on the base class. In any case, a C++ implementation for Perceptron processing nodes could be:
class perceptron_pe : public pe
{
public:
DATA threshold_function(DATA value)
{
if(value>0) return 1;
return 0;
}
};
(b) Next you may want to define a class for layers consisting of “perceptron_pe” objects as defined above; this can be done quickly using the template “Layer”:typedef Layer< perceptron_pe > perceptron_layer;(c) Moving on to the connections now. Notice that in Perceptron connections are the only elements modified (updating their weights) during encoding. Among other functionality, each connection knows its source and destination nodes, maintains and updates the weight, modifies transferred data etc. So a C++ class for such Percepton connections could be:
class perceptron_connection: public connection
{
public:
// mapping, multiply value coming from source node by weight
// and send it to destination node.
void recall()
{
destin_pe().receive_input_value( weight() * source_pe().output );
}
// training, weights are updated:
void encode()
{
weight() = weight() + 0.3 * (destin_pe().input - destin_pe().output) * source_pe().output;
}
};
for simplicity, during training learning rate is fixed to 0.3 and the connection assumes that the desired output values will be placed in the “input” registers of the destination nodes before updating weights.Note: for compatibility with nnlib2Rcpp version 0.1.4 (the current version on CRAN)- the example above assumes that the desired values are placed as input to the processing nodes right before update of weights (encoding); version 0.1.5 and above provides direct access from R to the “misc” variables that nodes and connections maintain (via “NN” method “set_misc_values_at”, more on “NN” below). It may have been more elegant to use these “misc” variables for holding desired output in processing nodes instead of “input”.
(d) Next, you may want to define a class for groups of such connections, which can be done quickly using the template “Connection_Set”:
typedef Connection_Set< perceptron_connection > perceptron_connection_set;Step 3: Add the ability to create such components at run-time.
Again in the “additional_parts.h” C++ header file found in directory “src” add code that creates Percepron layers and groups of connections when a particular name is used. Locate the “generate_custom_layer” function and add to it the line:
if(name == "perceptron") return new perceptron_layer(name,size);(you will notice other similar definitions are already there). Finally, locate the “generate_custom_connection_set” function and add to it the line:
if(name == "perceptron") return new perceptron_connection_set(name);(again, you will notice other similar definition examples are already there).
Note: as of July 15, 2020 all the aforementioned changes to “additional_parts.h” C++ header are already implemented as an example in the nnlib2Rcpp version 0.1.5 github repo [5].
That is it. You can now build the modified library and then return to the R world to use your newly created Perceptron components in a NN. The “NN” R module in nnlib2Rcpp allows you to combine these (and other) components in a network and then use it in R.
It is now time to see if this cut-down modified Perceptron is any good. In the example below, the iris dataset is used to train it. The example uses the “NN” R module in nnlib2Rcpp to build the network and then trains and tests it. The network topology consists of a generic input layer (component #1) of size 4 i.e. as many nodes as the iris features, a set of connections (component #2) whose weights are initialized to 0 (in create_connections_in_sets) below, and a processing layer (component #3) of size 3 i.e. as many nodes as the iris species:
library("nnlib2Rcpp")
# create the NN and define its components
p <- new("NN")
p$add_layer("generic",4)
p$add_connection_set("perceptron")
p$add_layer("perceptron",3)
p$create_connections_in_sets(0,0)
# show the NN topology
p$outline()
# prepare some data based on iris dataset
data_in <- as.matrix(iris[1:4])
iris_cases <- nrow((data_in))
species_id <- unclass(iris[,5])
desired_data_out <- matrix(data=0, nrow=iris_cases, ncol=3)
for(c in 1:iris_cases) desired_data_out[c,species_id[c]]=1
# encode data and desired output (for 30 training epochs)
for(i in 1:30)
for(c in 1:iris_cases)
{
p$input_at(1,data_in[c,])
p$recall_all(TRUE)
p$input_at(3,desired_data_out[c,])
p$encode_at(2)
}
# show the NN
p$print()
# Recall the data to see what species Perceptron returns:
for(c in 1:iris_cases)
{
p$input_at(1,data_in[c,])
p$recall_all(TRUE)
cat("iris case ",c,", desired = ", desired_data_out[c,], " returned = ", p$get_output_from(3),"\n")
}
Checking the output one sees that our Perceptron variation is not THAT bad. At least it recognizes Iris setosa and virginica quite well. However, classification performance on versicolor cases is rather terrible.iris case 1 , desired = 1 0 0 returned = 1 0 0
iris case 2 , desired = 1 0 0 returned = 1 0 0
iris case 3 , desired = 1 0 0 returned = 1 0 0
…
iris case 148 , desired = 0 0 1 returned = 0 0 1
iris case 149 , desired = 0 0 1 returned = 0 0 1
iris case 150 , desired = 0 0 1 returned = 0 0 1
Anyway, this example was not about classification success but about creating a new NN type in the nnlib2Rcpp R package. I hope it will be useful to some of you out there.
Links (all accessed July 12, 2020):
[1] Perceptron:
https://en.wikipedia.org/w/index.php?title=Perceptron&oldid=961536136
[2] RTools:
https://cran.r-project.org/bin/windows/Rtools/history.html
[3] Rcpp package:
https://cran.r-project.org/web/packages/Rcpp/index.html
[4] nnlib2Rcpp package on CRAN:
https://cran.r-project.org/web/packages/nnlib2Rcpp/index.html
[5] nnlib2Rcpp package on github:
https://github.com/VNNikolaidis/nnlib2Rcpp
[6] Frank Rosenblatt:
https://en.wikipedia.org/wiki/Frank_Rosenblatt
PS. Time permitting, more components will be added to the collection (and added to nnlib2Rcpp), maybe accompanied by posts similar to this one; these will eventually be available in the package. Any interesting or useful NN component that you would like to contribute is welcomed (credit, of course, will go to you, its creator); if so, please contact me using the comments below. (Another project is to create parallel-processing versions of the components, if anyone wants to help).
A single loop is not enough. A collection of hello world control structures
As the post on “hello world” functions has been quite appreciated by the R community, here follows the second round of functions for wannabe R programmer.
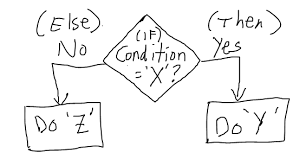
# If else statement:
# See the code syntax below for if else statement
x=10
if(x>1){
print(“x is greater than 1”)
}else{
print(“x is less than 1”)
}
# See the code below for nested if else statement
x=10
if(x>1 & x<7){
print(“x is between 1 and 7”)} else if(x>8 & x< 15){
print(“x is between 8 and 15”)
}
# For loops:
# Below code shows for loop implementation
x = c(1,2,3,4,5)
for(i in 1:5){
print(x[i])
}
# While loop :
# Below code shows while loop in R
x = 2.987
while(x <= 4.987) {
x = x + 0.987
print(c(x,x-2,x-1))
}
# Repeat Loop:
# The repeat loop is an infinite loop and used in association with a break statement.
# Below code shows repeat loop:
a = 1
repeat{
print(a)
a = a+1
if (a > 4) {
break
}
}
# Break statement:
# A break statement is used in a loop to stop the iterations and flow the control outside of the loop.
#Below code shows break statement:
x = 1:10
for (i in x){
if (i == 6){
break
}
print(i)
}
# Next statement:
# Next statement enables to skip the current iteration of a loop without terminating it.
#Below code shows next statement
x = 1: 4
for (i in x) {
if (i == 2){
next
}
print(i)
}
# function
words = c(“R”, “datascience”, “machinelearning”,”algorithms”,”AI”)
words.names = function(x) {
for(name in x){
print(name)
}
}
words.names(words) # Calling the function
# extract the elements above the main diagonal of a (square) matrix
# example of a correlation matrix
cor_matrix <- matrix(c(1, -0.25, 0.89, -0.25, 1, -0.54, 0.89, -0.54, 1), 3,3)
rownames(cor_matrix) <- c(“A”,”B”,”C”)
colnames(cor_matrix) <- c(“A”,”B”,”C”)
cor_matrix
rho <- list()
name <- colnames(cor_matrix)
var1 <- list()
var2 <- list()
for (i in 1:ncol(cor_matrix)){
for (j in 1:ncol(cor_matrix)){
if (i != j & i<j){
rho <- c(rho,cor_matrix[i,j])
var1 <- c(var1, name[i])
var2 <- c(var2, name[j])
}
}
}
d <- data.frame(var1=as.character(var1), var2=as.character(var2), rho=as.numeric(rho))
d
var1 var2 rho
1 A B -0.25
2 A C 0.89
3 B C -0.54
As programming is the best way to learn and think, have fun programming awesome functions! This post is also shared in R-bloggers and LinkedIn
Introduction to mebootSpear() Function
In the latest version of
The desired properties from the original maximum entropy bootstrap function
AirPassengers
The following example will demonstrate the
Reference
The following paper is available with additional examples and R-code:
Vinod, Hrishikesh D. and Viole, Fred, Arbitrary Spearman’s Rank Correlations in Maximum Entropy Bootstrap and Improved Monte Carlo Simulations (June 7, 2020). Available at SSRN: https://ssrn.com/abstract=3621614
meboot (v 1.4-8) on CRAN, the function mebootSpear was introduced. Below is a gentle introduction to its capabilities and a link to a reference paper with further applications to improved Monte Carlo simulations.The desired properties from the original maximum entropy bootstrap function
meboot were retained, while incorporating the additional argument setSpearman. The original function created bootstrap replicates with unit rank-correlations to the original time-series, setSpearman relaxes this condition.AirPassengers
The following example will demonstrate the
mebootSpear rank-correlation results from the average of 1,000 bootstrap replicates of the AirPassengers dataset.library(meboot)
output <- mebootSpear(AirPassengers, setSpearman = 0, xmin = 0)$rowAvgcor(output, AirPassengers, method = "spearman")
[1] 0.01695065Reference
The following paper is available with additional examples and R-code:
Vinod, Hrishikesh D. and Viole, Fred, Arbitrary Spearman’s Rank Correlations in Maximum Entropy Bootstrap and Improved Monte Carlo Simulations (June 7, 2020). Available at SSRN: https://ssrn.com/abstract=3621614
3D route visualisation – Kilimanjaro
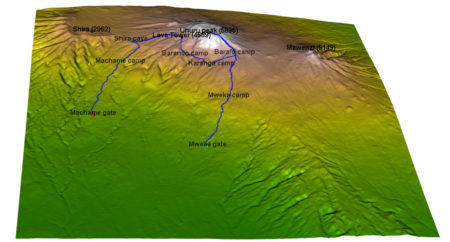
I will show here how to create an interactive 3D visualisation of geospatial data, using rgl library, that allows export of the results into HTML.
The dataset to visualize, is a 7 day hike to Kilimajaro mountain (5895 metres) in Tanzania.
Dataset contains latitude, longitude and elevation at sequence of timestamps.
route <- readr::read_delim("https://raw.githubusercontent.com/mvhurban/kilimanjaro/master/Kilimanjaro_ascent.csv", ";", escape_double = FALSE, trim_ws = TRUE)
The elevation gain of hiker in meters can be plotted simply:plot(route$ele)
When visualizing small areas, such as cities, mountains or parts of countries, distortion due to Geoid projection on 2D surface is insignificant and it is sufficient to set the projection center to the visualized area. Our dataset falls into this category and therefore can be bounded by:
max_lat = max(route$lat) min_lat = min(route$lat) max_lon = max(route$lon) min_lon = min(route$lon)To create a 3D surface, units must match altitude units (meters). This can be achieved by scaling coordinates by factor corresponding to the arclength of
latitude or longitude degree:
We can use function distGeo (this calculates great circle distance between two points on Earth) to obtain conversion scales.
library(geosphere) library(rgdal) lon_scale = geosphere::distGeo(c(min_lon, (min_lat+max_lat)/2), c(max_lon,(min_lat+max_lat)/2))/(max_lon-min_lon) lat_scale = geosphere::distGeo(c(min_lon, min_lat), c(min_lon, max_lat))/(max_lat-min_lat)By hving conversion scales for latitude and logitude, we can convert GPS coordinates to cartesian coordinates in the plane tangent to the Earth at the center of the dataset. One can see it as placing a sheet of paper on the scrutinized spot on Earth.
route$lon_m <- route$lon * lon_scale route$lat_m <- route$lat * lat_scaleTo obtain the elevation data surrounding the track we define a polygon (rectangle) enclosing the track. Note, that the polygon ends and begins with same point.
y_coord <- c(min_lat, min_lat, max_lat, max_lat, min_lat) # latitude x_coord <- c(min_lon, max_lon, max_lon, min_lon, min_lon) # longitudeGeospatial polygons can be handled by sp library. Such a polygon must contain a projection string prj_sps defining how to interpret coordinates:
library(sp)
polygon_border <- cbind(x_coord, y_coord)
p <- sp::Polygon(polygon_border)
ps <- sp::Polygons(list(p), 1)
sps <- sp::SpatialPolygons(list(ps))
prj_sps <- sp::CRS("+proj=longlat +datum=WGS84 +no_defs +ellps=WGS84 +towgs84=0,0,0")
sp::proj4string(sps) <- prj_sps
spdf = sp::SpatialPolygonsDataFrame(sps, data.frame(f=99.9))
#plot(spdf)
We define grid with points at which elevation data will be requested. Then we define projection string for a grid object:grid_data <- sp::makegrid(spdf, cellsize = 0.001) # cellsize in map units (here meters)! grid <- sp::SpatialPoints(grid_data, proj4string = prj_sps)The Elevation data for raster object can be downloaded using elevatr library by to accessing the Terrain Tiles on AWS.
library(elevatr) elevation_df <- elevatr::get_elev_raster(grid, prj = prj_sps, z = 12) #plot(elevation_df)Transforming raster object to dataframe:
library(raster) kili_map <- as.data.frame(raster::rasterToPoints(elevation_df))Since we have equidistant rectangular grid, we can rearrange points into matrix and project to the plane:
lenX = length(unique(kili_map$x)) lenY = length(unique(kili_map$y)) z_full = matrix(kili_map$layer, nrow=lenX, ncol =lenY, byrow = FALSE ) x_full = lon_scale * matrix(kili_map$x, nrow=lenX, ncol =lenY, byrow = FALSE ) # longitude y_full = lat_scale * matrix(kili_map$y, nrow=lenX, ncol =lenY, byrow = FALSE ) # latitudeAt this stage, it is possible to generate 3D model of route, but depending on the dataset, additional problems may occur.
Here we address mismatch of Track altitudes and of the altitude dowloaded using elevatr library.
I our case elevations do not match and some points of Kilimanjaro dataset are above and some below elevatr altitudes and this overlap makes the display ugly.
We solve this problem by discarding provided elevations and projecting GPS coordinates to dowloaded grid. (Another option would be to use elevatr::get_elev_point(), which returns altitude for the dataframe.)
The projection is done by finding the closest point on a grid to the route point and assigning the elevation, the search of closest neighbour is done by a function provided in data.table library:
library(data.table)
dt_route = data.table::data.table(route)
N = nrow(dt_route)
data.table::setkeyv(dt_route, c('lon_m','lat_m'))
coor_x = data.table::data.table(ind_x=c(1:lenX), lon_m=x_full[ , 1])
coor_y = data.table::data.table(ind_y=c(1:lenY),lat_m=y_full[1, ])
dt_route$ind_y = coor_y[dt_route, on = 'lat_m', roll='nearest']$ind_y
dt_route$ind_x = coor_x[dt_route, on = 'lon_m', roll='nearest']$ind_x
for (i in c(1:N)){
dt_route$altitude[i]<-z_full[dt_route$ind_x[i], dt_route$ind_y[i]]}
For our purposes, the size of grid object is too big and we can skip few points:Note that skipping every 5 grid points makes a reduction of the size by 96%!
skip_cell = 5 x = x_full[seq(1, lenX, by=skip_cell), seq(1, lenY, by=skip_cell)] y = y_full[seq(1, lenX, by=skip_cell), seq(1, lenY, by=skip_cell)] z = z_full[seq(1, lenX, by=skip_cell), seq(1, lenY, by=skip_cell)]Colors can be assigned to a particular altitude by color pallet, for obvious reasons we have choosen terrain.colors. But since Kilimanjaro has snow above 5300 m, we added the snowline.
snowline <- 5300 # above this line color will be white colorlut <- terrain.colors(snowline-0, alpha = 0) # maping altitude to color: minimum is 0 - green, maximum 5300 - white z_col<-z z_col[z_col>snowline] <- snowline col <- colorlut[z_col]Calculating relative time spent on the hike:
dt_route = dt_route[order(time), ] time <- as.POSIXlt(dt_route$time, format='%Y-%m-%d-%H-%M-%S') start_time = time[1] end_time = time[N] dt_route$relative_time <- as.numeric(difftime(time, start_time, units ='hours'))/as.numeric(difftime(end_time, start_time, units='hours'))Here we add some additional perks to the map:
#### CAMPS
camp_index<-c(1, 2897, 4771, 7784, 9275, 10396,15485, 17822)
camp_lon <- dt_route[camp_index, lon_m]
camp_lat <- dt_route[camp_index, lat_m]
camp_alt <- dt_route[camp_index, altitude]
camp_names <- c('Machame gate','Machame camp', 'Shira cave', 'Baranco camp', 'Karanga camp', 'Barafu camp', 'Mweka camp', 'Mweka gate')
#### PEAKS
peak_lon <- lon_scale*c( 37.3536381, 37.4561200, 37.3273936, 37.2370328)
peak_lat <- lat_scale*c(-3.0765783, -3.0938911, -3.0679128, -3.0339558)
peak_alt <- c(5895, 5149, 4689, 2962)-50
peak_names<-c("Uhuru peak (5895)", "Mawenzi (5149)", "Lava Tower (4689)", "Shira (2962)")
#### Hike
skip_points <- 10
aux_index <- seq(1, N, by=skip_points)
time <- dt_route[aux_index, relative_time]
hike <- cbind(dt_route[aux_index, lon_m], dt_route[aux_index, lat_m], dt_route[aux_index, altitude])
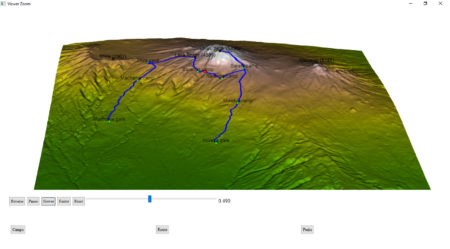
Finally, plotting using rgl library. It is important, that rgl window initialized by rgl::open3d() is open while objects are created. Each object created is loaded to html element within rgl scene3d, and at any moment can be saved as scene object by command: kilimanjaro_scene3d <- scene3d() (which assigns current status of rgl window). Note, that the importance of parameter alpha, where alpha=1 corresponds to non-transparent objects, while for display of texts the transparency is allowed, which smoothes imaging of edges (alpha=0.9).library(rmarkdown)
rgl::open3d()
hike_path <- rgl::plot3d(hike, type="l", alpha = 1, lwd = 4, col = "blue", xlab = "latitude", ylab='longitude', add = TRUE)["data"]
rgl::aspect3d("iso") # set equilateral spacing on axes
camp_shape <- rgl::spheres3d(camp_lon, camp_lat, camp_alt, col="green", radius = 150)
rgl::rgl.surface(x, z, y, color = col, alpha=1)
hiker <- rgl::spheres3d(hike[1, , drop=FALSE], radius = 200, col = "red")
camp_text<-rgl::rgl.texts(camp_lon, camp_lat, camp_alt+400,camp_names
, font = 2, cex=1, color='black', depth_mask = TRUE, depth_test = "always", alpha =0.7)
peak_shape <- rgl::spheres3d(peak_lon, peak_lat, peak_alt, col="black", radius = 150)
peak_text <- rgl::rgl.texts(peak_lon,peak_lat,peak_alt+400,peak_names
,font = 2, cex=1, color='black', depth_mask = TRUE, depth_test = "always", alpha =0.9)
To generate an interactive HTML, rgl library provides the rglwidget function, that can be used to display the motion of a hiker in real time. It is worth to mention how agecontrol object works: it generates a set of objects with predefined life cycle, where birth defines the time of spawn, age defines the vector of time periods (in object age) at which value of object changes like the transparency (alpha).library(rgl)
rgl::rglwidget() %>%
playwidget(
ageControl(births = 0, ages = time, vertices = hike, objids = hiker),step = 0.01, start = 0, stop=1, rate = 0.01, components = c("Reverse", "Play", "Slower", "Faster","Reset", "Slider", "Label"), loop = TRUE) %>%
toggleWidget(ids = c(camp_shape, camp_text), label="Camps") %>%
toggleWidget(ids = hike_path, label="Route") %>%
toggleWidget(ids = c(peak_shape, peak_text), label="Peaks") %>%
asRow(last = 3)
And that’s it!Version modified to satisfy requirements of Shiny apps is posted here:
https://mvhurban.shinyapps.io/GPS_zobrazovanie/
R code for removing Bias in Covid-19 data Using Econometric Tools
by H D Vinod and K Theiss
library(sampleSelection)
library(margins)
library(dplyr)
##Pull Data
Cumulative_Deaths=read.csv("Cumulative Deaths.csv")
Cumulative_Infections=read.csv("Cumulative Infections.csv")
Covid=read.csv("Covid_0615.csv")
##clean data
Covid$State.Abbreviation<-Covid$STA
Final_Dataset<-merge(Covid,Cumulative_Deaths,by="State.Abbreviation")
Data<-merge(Final_Dataset,Cumulative_Infections,by="State.Abbreviation")
2020/06/15: First Step Probit Model
myprobit<-glm(TI~HES+CPT+UI+HR+HI, family=binomial(link="probit"),data=Data)
##TI is Testing Indicator (i.e. 1 for tested and 0 for not tested)
##HES is Hospital Employee Share
##CPT is portion of population that Commutes on Public Transit
##UI in Uninsured Population
##HR is Hypertension Rate (one of the leading comorbidities)
#HI is Household Income
summary(myprobit)
##
## Call:
## glm(formula = TI ~ HES + CPT + UI + HR + HI, family = binomial(link = "probit"),
## data = Data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.7296 -0.3849 -0.3553 -0.3376 2.5180
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.4319390 0.0636110 -38.231 < 2e-16 ***
## HES 0.0663127 0.0081659 8.121 4.64e-16 ***
## CPT 0.0193450 0.0004345 44.523 < 2e-16 ***
## UI -0.0070335 0.0009966 -7.058 1.69e-12 ***
## HR 0.0198518 0.0011021 18.012 < 2e-16 ***
## HI 0.0021614 0.0004608 4.690 2.73e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 254187 on 499999 degrees of freedom
## Residual deviance: 250590 on 499994 degrees of freedom
## AIC: 250602
##
## Number of Fisher Scoring iterations: 5
2020/06/15: Probit Model Marginal Effects
#Marginal Effects of probit model
effects_pro=margins(myprobit) #print(effects_pro)
summary(effects_pro)
1 CPT 0.0025685341 5.801388e-05 44.274475 0.000000e+00 0.0024548290 0.0026822392
2 HES 0.0088046672 1.084429e-03 8.119170 4.693813e-16 0.0066792246 0.0109301098
3 HI 0.0002869787 6.119577e-05 4.689519 2.738481e-06 0.0001670372 0.0004069203
4 HR 0.0026358250 1.465264e-04 17.988742 2.387156e-72 0.0023486386 0.0029230114
5 UI -0.0009338730 1.323531e-04 -7.055923 1.714593e-12 -0.0011932802 -0.0006744657
5 rows
2020/06/15: Extract inverse Mills ratio from probit model
##Compute inverse Mills ratio from probit model usine 'invMillsRatio' command from the 'sampleSelection' package.
IMR=invMillsRatio(myprobit,all=FALSE)
Data$IMR<-invMillsRatio(myprobit)$IMR1
##create table of IMR values by state
IMR.Index=cbind(as.character(Data$State.Abbreviation),Data$IMR)
IMR_table=distinct(data.frame(IMR.Index))
2020/06/15: Second Step Heckman Equation (i.e. with IMR)
##GLM with Poisson distribution to estimate cumulative deaths based on the log of cumulative infections from the previous week, as well as the IMR.
##Use 'glm' command with 'family=poisson(link="log")'
##Only ran the model on individuals who were tested (i.e. TI = 1).
##CD is "Cumulative Deaths"
##CI is "Cumulative Infections"
glm_IMR_0615_CD<-glm(X20200615_CD~log(X20200608_CI)+IMR,family=poisson(link="log"),
data=subset(Data,TI==1))
fig-out-of-sample-all
#Compute fitted values for each state
Tested_Individuals<-subset(Data,TI==1)
Fitted_CD_IMR=fitted(glm_IMR_0615_CD)
Fitted_CD=fitted(glm_0615_CD)
Results_Table=cbind(as.character(Tested_Individuals$State.Abbreviation),Tested_Individuals$X20200622_CI,
Tested_Individuals$X20200622_CD,Tested_Individuals$X20200615_CD,Fitted_CD_IMR,Fitted_CD,
Tested_Individuals$IMR)
#Pull fitted value for each state
Final_Results=distinct(data.frame(Results_Table))
View(Final_Results)
Assessing Nation-wide Forecast
#Compare fitted values with in-sample (2020/06/15) and out-of-sample (2020/06/22) actual deaths
Actual_Infections_Out_Sample=sum(as.numeric(Final_Results[,2]))
Actual_Deaths_Out_Sample=sum(as.numeric(Final_Results[,3]))
Predict_Deaths_IMR=sum(as.numeric(Final_Results$Fitted_CD_IMR))
Predict_Deaths_no_IMR=sum(as.numeric(Final_Results$Fitted_CD))
Out_of_sample_per_diff_CD_IMR=(Predict_Deaths_IMR-Actual_Deaths_Out_Sample)/Actual_Deaths_Out_Sample
Out_of_sample_per_diff__CD_no_IMR=(Predict_Deaths_no_IMR-Actual_Deaths_Out_Sample)/Actual_Deaths_Out_Sample
Actual_Deaths_In_Sample=sum(as.numeric(Final_Results[,4]))
In_sample_per_diff_CD_IMR=(Predict_Deaths_IMR-Actual_Deaths_In_Sample)/Actual_Deaths_In_Sample
In_sample_per_diff_CD_no_IMR=(Predict_Deaths_no_IMR-Actual_Deaths_In_Sample)/Actual_Deaths_In_Sample
print(rbind(Actual_Deaths_In_Sample,In_sample_per_diff_CD_IMR,In_sample_per_diff_CD_no_IMR))
## [,1]
## Actual_Deaths_In_Sample 1.098220e+05
## In_sample_per_diff_CD_IMR 4.064085e-03
## In_sample_per_diff_CD_no_IMR -4.705036e-02
print(rbind(Actual_Infections_Out_Sample,Actual_Deaths_Out_Sample,Predict_Deaths_no_IMR, Out_of_sample_per_diff_CD_IMR,Out_of_sample_per_diff__CD_no_IMR))
## [,1]
## Actual_Infections_Out_Sample 2.290489e+06
## Actual_Deaths_Out_Sample 1.139440e+05
## Predict_Deaths_no_IMR 1.046548e+05
## Out_of_sample_per_diff_CD_IMR -3.225860e-02
## Out_of_sample_per_diff__CD_no_IMR -8.152394e-02
In all nine cases using IMR bias correction improves out-of-sample forecasts of Covid-19 deaths in US as a whole
cbind(Week,IMR_Perc_Diff,Without_IMR_Perc_Diff)
## Week IMR_Perc_Diff Without_IMR_Perc_Diff
## [1,] 1 -25.27 -26.96
## [2,] 2 -21.61 -22.50
## [3,] 3 -17.66 -18.73
## [4,] 4 -12.14 -13.78
## [5,] 5 -9.38 -11.28
## [6,] 6 -7.25 -9.70
## [7,] 7 -5.53 -9.01
## [8,] 8 -3.94 -8.03