The World of Anomalies
Imagine you are a credit card selling company and you know about a particular customer who makes a purchase of 25$ every week. You guessed this purchase is his fixed weekly rations but one day, this customer makes a different purchase of 700$. This development will not just startle you but also compel you to talk to the customer and find out the reason so you can approve the transaction. This is because, the behavior of the customer had become fixed and the change was so different that it was not expected. Hence we call this event as an anomaly.Anomalies are hard to detect because they can also be real phenomenon. Let’s say that the customer in the example above made the usual purchases while he was living alone and will be starting his family this week. This will mean that this should be the first of his future purchases of similar magnitude or he is throwing a party this week and this was a one-time large purchase. In all these cases, the customer will be classified as making an ‘abnormal’ choice. We as the credit card seller need to know which of these cases are genuine and which are mistakes which can be corrected if they reconfirm the same with the customer. The usefulness of detecting such anomalies are very useful especially in BFSI industry with the primary use in credit card transactions. Such anomalies can be signs of fraud or theft. Someone making multiple transactions of small amounts from the same credit card, making one very large transaction which is a few order of magnitudes larger than the average, making transactions from an unfamiliar location are such examples that can caused by fraudsters and must be caught. With the popularity of adoption, let’s study the ways we can detect anomalies.
Detecting The Pattern To Find Anomalies
Anomalies are essentially the outliers in our data. If something happens regularly, it is not an anomaly but a trend. Things which happen once or twice and are deviant from the usual behavior, whether continuously or with lags are all anomalies. So it all boils down to the definition of outliers for our data. R provides a lot of packages with different approaches to anomaly detection. We will use the AnomalyDetection package in R to understand the concept of anomalies using one such method. However, the package needs to be installed specially from github. This requires the install_github() function in devtools package. We will also use the Rcpp package which helps us to integrate R with C++ functions. Another github package to be used in this article is the wikipedia trend package which contains the API to access wikipedia and create data for anomaly detection analysis.The package is capable of identifying outliers in the presence of seasonality and trend in the data. The package uses an algorithm known as Seasonal Hybrid ESD algorithm which finds outliers globally as well as locally in time series or a vector of data. The package has a lot of features, some of which include visualization graphs, type of anomalies (positive or negative) and specifying the window of interest.
#Install the devtools package then github packages
install.packages("devtools")
install.packages("Rcpp")
library(devtools)
install_github("petermeissner/wikipediatrend")
install_github("twitter/AnomalyDetection")
#Loading the libraries
library(Rcpp)
library(wikipediatrend)
library(AnomalyDetection)
The first step is data preparation. We will use the page views on wikipedia page marked on fifa data starting from date 18th March 2013. (link: https://en.wikipedia.org/wiki/FIFA). The wp_trend function gives us the access statistics for the page with the ability to filter data from within the function. We will use this data to model day wise page views and understand anomalies in the pattern of those view numbers
#Download wikipedia webpage "fifa"
fifa_data_wikipedia = wp_trend("fifa", from="2013-03-18", lang = "en")
This gives us a dataset of about 1022 observations and 8 columns. Looking at the data reveals some redundant information captured
#First_look fifa_data_wikipedia project language article access agent granularity date views 197 wikipedia en Fifa all-access all-agents daily 2016-01-13 116 546 wikipedia en Fifa all-access all-agents daily 2016-12-27 64 660 wikipedia en Fifa all-access all-agents daily 2017-04-20 100 395 wikipedia en Fifa all-access all-agents daily 2016-07-29 70 257 wikipedia en Fifa all-access all-agents daily 2016-03-13 75 831 wikipedia en Fifa all-access all-agents daily 2017-10-08 194 229 wikipedia en Fifa all-access all-agents daily 2016-02-14 84 393 wikipedia en Fifa all-access all-agents daily 2016-07-27 140 293 wikipedia en Fifa all-access all-agents daily 2016-04-18 105 420 wikipedia en Fifa all-access all-agents daily 2016-08-23 757We see that project, language, article, access, agent and granularity appear to be same for all rows and are irrelevant for us. We are only concerned with date and views as the features to work on. Let’s plot the views against date
#Plotting data library(ggplot2) ggplot(fifa_data_wikipedia, aes(x=date, y=views, color=views)) + geom_line()
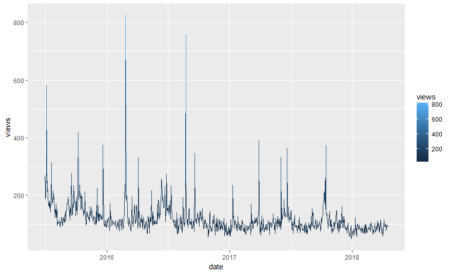
We see some huge spikes at different intervals. There are a lot of anomalies in this data. Before we process them further, let’s keep only the relevant columns.
# Keep only date & page views and discard all other variables
columns_to_keep=c("date","views")
fifa_data_wikipedia=fifa_data_wikipedia[,columns_to_keep]
We will now perform anomaly detection using Seasonal Hybrid ESD Test. The technique maps data as a series and captures seasonality while pointing out data which does not follow the seasonality pattern. The AnomalyDetectionTs() function finds the anomalies in the data. It will basically narrow down all the peaks keeping in mind that not more than 10% of data can be anomalies (by default). We can also reduce this number by changing the max_anoms parameter in the data. We can also specify which kind of anomalies are to be identified using the direction parameter. Here, we are going to specify only positive direction anomalies to be identified. That means that sudden dips in the data are not considered.
#Apply anomaly detection and plot the results anomalies = AnomalyDetectionTs(fifa_data_wikipedia, direction="pos", plot=TRUE) anomalies$plot
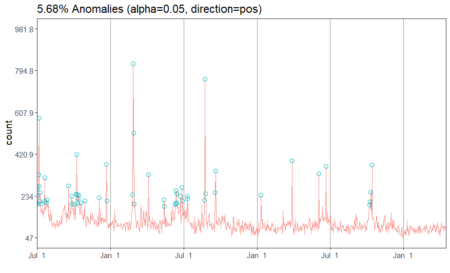
Our data has 5.68% anomalies in positive direction if we take a level of significance (alpha) to be 95%. Since we had a total of 1022 observations, 5.68% of the number is about 58 observations. We can look at the specific dates which are pointed out by the algorithm.
# Look at the anomaly dates anomalies$anoms timestamp anoms 1 2015-07-01 269 2 2015-07-02 233 3 2015-07-04 198 4 2015-07-05 330 5 2015-07-06 582 6 2015-07-07 276 7 2015-07-08 211 8 2015-07-09 250 9 2015-07-10 198 10 2015-07-20 315 11 2015-07-21 209 12 2015-07-25 202 13 2015-07-26 217 14 2015-09-18 278 15 2015-09-25 234 16 2015-09-26 199 17 2015-10-03 196 18 2015-10-07 242 19 2015-10-08 419 20 2015-10-09 240 21 2015-10-11 204 22 2015-10-12 223 23 2015-10-13 237 24 2015-10-18 204 25 2015-10-28 213 26 2015-12-03 225 27 2015-12-21 376 28 2015-12-22 212 29 2016-02-24 240 30 2016-02-26 826 31 2016-02-27 516 32 2016-02-29 199 33 2016-04-04 330 34 2016-05-13 217 35 2016-05-14 186 36 2016-06-10 196 37 2016-06-11 200 38 2016-06-12 258 39 2016-06-13 245 40 2016-06-14 204 41 2016-06-22 232 42 2016-06-27 273 43 2016-06-28 212 44 2016-07-10 221 45 2016-07-11 233 46 2016-08-22 214 47 2016-08-23 757 48 2016-08-24 244 49 2016-09-18 250 50 2016-09-19 346 51 2017-01-10 237 52 2017-03-29 392 53 2017-06-03 333 54 2017-06-21 365 55 2017-10-08 194 56 2017-10-09 208 57 2017-10-11 251 58 2017-10-14 373We have the exact dates and the anomaly values for each date. In a typical anomaly detection process, each of these dates are looked case by case and the reason for anomalies is identified. For instance, the page views can be higher on these dates if there had been fifa matches or page updates on these particular days. Another reason could be big news about fifa players. However, if page views on any of the dates does not correspond to any special event, then those days are true anomalies and should be flagged. In other situations such as credit card transactions, such anomalies can indicate fraud and quick action must be taken on identification.
The ‘Anomaly Way’
Anomalies are a kind of outlier so SH-ESD (Seasonal Hybrid ESD) is not the only way to detect anomalies. Moreover, ‘AnomalyDetection’ is not the only package we will look upon. Let’s try the anomalize package which is available in CRAN. However, it is always recommended to update the package using github as the owners keep the most recent package versions there and it takes time and testing for the changes to move into standard repositories such as CRAN. We will first install the package from CRAN so that the dependencies are also installed then update the package using devtools#Installing anomalize
install.packages('anomalize')
#Update from github
library(devtools)
install_github("business-science/anomalize")
#Load the package
library(anomalize)
# We will also use tidyverse package for processing and coindeskr to get bitcoin data
library(tidyverse)
library(coindeskr)
I am also using the tidyverse package (Link) and coindeskr package (Link). The coindeskr package is used to download the bitcoin data and tidyverse is used for speedy data processing. We will now download bitcoin data from 1st January 2017
#Get bitcoin data from 1st January 2017 bitcoin_data <- get_historic_price(start = "2017-01-01")This data indicates the price per date. Let’s convert it into a time series
#Convert bitcoin data to a time series
bitcoin_data_ts = bitcoin_data %>% rownames_to_column() %>% as.tibble() %>% mutate(date = as.Date(rowname)) %>% select(-one_of('rowname'))
In the time series conversion, we are actually converting the data to a tibble_df which the package requires. We could have alternatively converted the data into tibbletime object. Since it is a time series now, we should also see the seasonality and trend patterns in the data. It is important to remove them so that anomaly detection is not affected. We will now decompose the series. We will also plot the series #Decompose data using time_decompose() function in anomalize package. We will use stl method which extracts seasonality
bitcoin_data_ts %>% time_decompose(Price, method = "stl", frequency = "auto", trend = "auto") %>% anomalize(remainder, method = "gesd", alpha = 0.05, max_anoms = 0.1) %>% plot_anomaly_decomposition() Converting from tbl_df to tbl_time. Auto-index message: index = date frequency = 7 days trend = 90.5 days
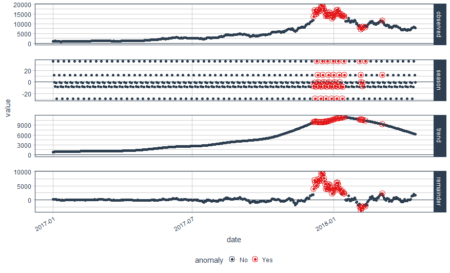
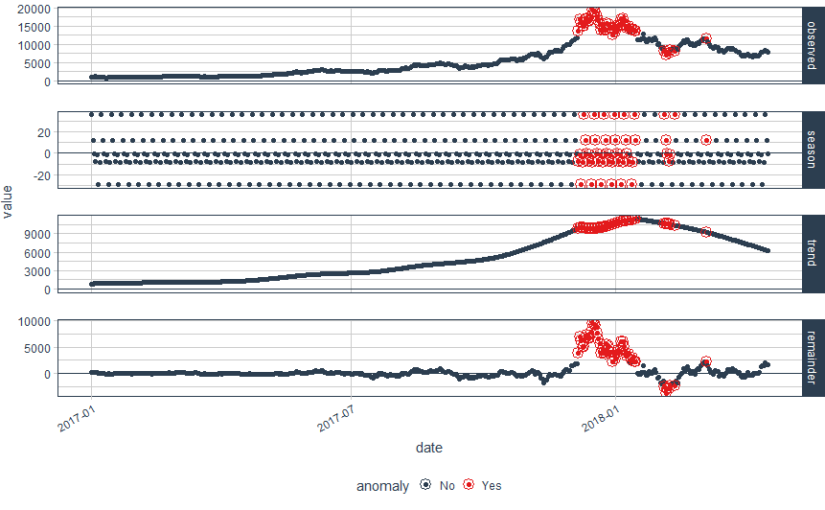
We have some beautiful plots with the first plot being overall observed data, second being season, third being trend and the final plot analyzed for anomalies. The red points indicate anomalies according to the anomalize function. However, we are not looking for this plot. We only want the anomalies plot with trend and seasonality removed. Let’s plot the data again with recomposed data. This can be done by setting the time_recomposed() function
#Plot the data again by recomposing data
bitcoin_data_ts %>% time_decompose(Price) %>% anomalize(remainder) %>% time_recompose() %>% plot_anomalies(time_recomposed = TRUE, ncol = 3, alpha_dots = 0.5) Converting from tbl_df to tbl_time. Auto-index message: index = date frequency = 7 days trend = 90.5 days
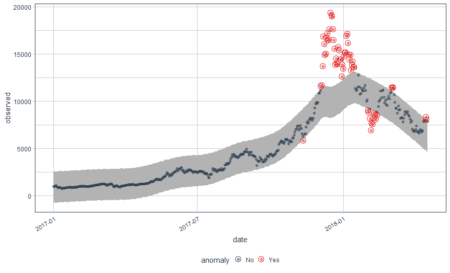
This is a better plot and shows the anomalies. We all know how bitcoin prices shot up in 2018. The grey portion explains the expected trend. Let’s see what these red points are.
#Extract the anomalies anomalies=bitcoin_data_ts %>% time_decompose(Price) %>% anomalize(remainder) %>% time_recompose() %>% filter(anomaly == 'Yes')Now the anomalies dataset consists of the data points which were identified as anomalies by the algorithm
Conclusion: Are You An Anomaly?
We have twitter’s anomaly detection package based on Seasonal Hybrid ESD (SH-ESD) as well as CRAN’s anomaly detection package based on factor analysis, Mahalanobis distance, Horn’s parallel analysis or Principal component analysis. We also have TsOutliers package and anomalize packages in R. There are a lot more packages than one could find in R. They all have the same concept but differ in the underlying algorithm which they use to detect anomaly. Hence, one can get a general idea from all such packages: anomalies are data points which do not follow the general trend or do not lie under the expected behavior of the rest of the data. The next question which is raised is the criteria for a data point to be following expected behavior. The rest of the data points are all anomalies. One can also have varying types of anomalies such as direction based anomalies as described by the anomaly detection package (positive or negative) or anomalies not following events such as matches in fifa data. One can similarly pitch in another logic for anomaly classification and treat them accordingly.Here is the entire code used in this article
#Install the devtools package then github packages
install.packages("devtools")
install.packages("Rcpp")
library(devtools)
install_github("petermeissner/wikipediatrend")
install_github("twitter/AnomalyDetection")
#Loading the libraries
library(Rcpp)
library(wikipediatrend)
library(AnomalyDetection)
# Download wikipedia webpage "fifa"
fifa_data_wikipedia = wp_trend("fifa", from="2013-03-18", lang = "en")
#First_look
fifa_data_wikipedia
# Plotting data
library(ggplot2)
ggplot(fifa_data_wikipedia, aes(x=date, y=views, color=views)) + geom_line()
# Keep only date & page views and discard all other variables
columns_to_keep=c("date","views")
fifa_data_wikipedia=fifa_data_wikipedia[,columns_to_keep]
#Apply anomaly detection and plot the results
anomalies = AnomalyDetectionTs(fifa_data_wikipedia, direction="pos", plot=TRUE)
anomalies$plot
# Look at the anomaly dates
anomalies$anoms
#Installing anomalize
install.packages('anomalize')
#Update from github
library(devtools)
install_github("business-science/anomalize")
#Load the package
library(anomalize)
# We will also use tidyverse package for processing and coindeskr to get bitcoin data
library(tidyverse)
library(coindeskr)
#Get bitcoin data from 1st January 2017
bitcoin_data = get_historic_price(start = "2017-01-01")
#Convert bitcoin data to a time series
bitcoin_data_ts = bitcoin_data %>% rownames_to_column() %>% as.tibble() %>% mutate(date = as.Date(rowname)) %>% select(-one_of('rowname'))
#Decompose data using time_decompose() function in anomalize package. We will use stl method which extracts seasonality
bitcoin_data_ts %>% time_decompose(Price, method = "stl", frequency = "auto", trend = "auto") %>% anomalize(remainder, method = "gesd", alpha = 0.05, max_anoms = 0.1) %>% plot_anomaly_decomposition()
#Plot the data again by recomposing data
bitcoin_data_ts %>% time_decompose(Price) %>% anomalize(remainder) %>% time_recompose() %>% plot_anomalies(time_recomposed = TRUE, ncol = 3, alpha_dots = 0.5)
#Extract the anomalies
anomalies=bitcoin_data_ts %>% time_decompose(Price) %>% anomalize(remainder) %>% time_recompose() %>% filter(anomaly == 'Yes')





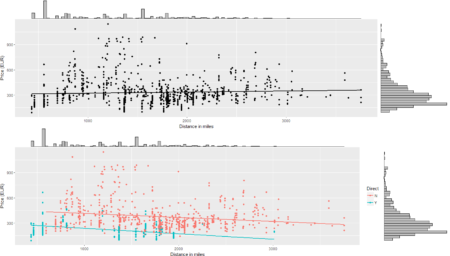 To conclude the 4-step (flight) trip from data acquisition to data analysis, let's recap the most important concepts described in each of the post:
1)
To conclude the 4-step (flight) trip from data acquisition to data analysis, let's recap the most important concepts described in each of the post:
1) 
 The collection of example flight data in json format available in
The collection of example flight data in json format available in 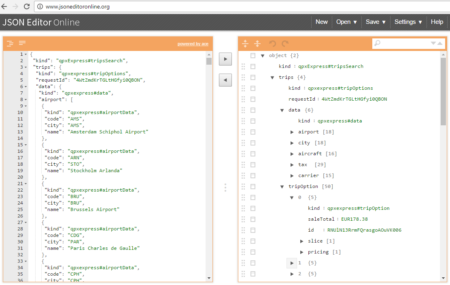 However, looking deeply into the object, several other elements are provided as the distance in mile, the segment, the duration, the carrier, etc. The R parser to transform the json structure in a usable dataframe requires the dplyr library for using the pipe operator (%>%) to streamline the code and make the parser more readable. Nevertheless, the library actually wrangling through the lines is tidyjson and its powerful functions:
However, looking deeply into the object, several other elements are provided as the distance in mile, the segment, the duration, the carrier, etc. The R parser to transform the json structure in a usable dataframe requires the dplyr library for using the pipe operator (%>%) to streamline the code and make the parser more readable. Nevertheless, the library actually wrangling through the lines is tidyjson and its powerful functions: