Introduction to Looping system
Imagine you were to perform a simple task, let’s say calculating sum of columns for 3X3 matrix, what do you think is the best way? Calculating it directly using traditional methods such as calculator or even pen and paper doesn’t sound like a bad approach. A lot of us may prefer to just calculate it manually instead of writing an entire piece of code for such a small dataset.
Now, if the dataset is 10X10 matrix, would you do the same? Not sure.
Now, if the dataset is further bigger, let’s say 100X100 matrix or 1000X1000 matrix or 5000X5000 matrix, would you even think of doing it manually? I won’t.
But, let’s not worry ourselves with this task because it is not as big a task as it may look at prima facie. There’s a concept called ‘looping’ which comes to our rescue in such situations. I’m sure whosoever has ever worked on any programming language, they must have encountered loops and looping system. It is one of the most useful concepts in any programming language. ‘Looping system’ is nothing but an iterative system that performs a specific task repeatedly until given conditions are met or it is forced to break. Looping system comes in handy when we have to carry a task iteratively; we may or may not know before-hand how many iterations to be carried out. Instead of writing the same piece of code tens or hundreds or thousands of times, we write a small piece of code using loops and it does the entire task for us.
There are majorly two loops which are used extensively in programming – for loop and while loop. In the case of ‘for loop’ we know before hand as to how many times we want the loop to run or we know before-hand the number of iterations that should be carried out. Let’s take a very simple example of printing number 1 to 10. One way could be we write the code of printing every number from 1 to 10; while, the other and smart way would be to write a two-line code that will do the work for us.
for (i in 1:10) {
print(i)
}
The above code should print values from 1 to 10 for us.
> for (i in 1:10) {
+ print(i)
+ }
[1] 1
[1] 2
[1] 3
[1] 4
[1] 5
[1] 6
[1] 7
[1] 8
[1] 9
[1] 10
The other very powerful loop is ‘while’ loop. In while loop, we don’t know before-hand as to how many iterations should the loop perform. It works till a certain condition is being met, as soon as the condition is violated the loop breaks.
i = 1
while (i < 10) {
print(i)
i = i+1
}
In the above code, we don’t know how many iterations are there, we just know that the loop should work until the value of ‘i’ is less than 10 and it does the same.
> i = 1
> while (i < 10) {
+ print(i)
+ i = i+1
+ }
[1] 1
[1] 2
[1] 3
[1] 4
[1] 5
[1] 6
[1] 7
[1] 8
[1] 9
Using very basic examples, we have seen how powerful these loops can be. However, there is one disadvantage of using these loops in R language – they make our code run slow. The number of computations that needs to be carried increases and this increases the time that system takes to execute the code.
But we need not worry about this limitation as R offers a very good alternative, vectorization, to using these loops in lot of conditions. Vectorization, as the name suggests, is an operation of converting scalars or plain numbers in to single operation on vectors or matrices. A lot of functions that are performed by loops can be performed through vectorization. Moreover, vectorization makes calculation and running of processes faster because they convert the code into lower language such as C, C++ which further contains loops to execute the operation. User need not worry about these aspects of vectorization and can just do fine with direct functions.
Based on the concept of vectorization is a family of functions in R called ‘apply’ family function. It is a part of base R package. There are multiple functions in the apply family. We will go through them one by one and check their implementation, alongside, in R. The functions in apply family are apply, sapply, lapply, mapply, rapply, tapply and vapply. Their usage depends on the kind of input data we have, kind of output we want to see and the kind of operations we want to perform on data. Let’s go through some of these functions and implement toy examples using them.
Apply Function
Apply function is the most commonly used function in apply family. It works on arrays or matrices. The syntax of apply function is follows:
Apply(x, margin, function, ….)
Where,
- X refers to an array or matrix on which operation is to be performed
-
Margin refers to how the function is to be applied; margin =1 means function is to be applied on rows, while margin = 2 means function is to be applied on columns. Margin = c(1,2) means function is to be applied on both row and column.
-
Function refers to the operation that is to be performed on the data. It could be predefined functions in R such as Sum, Stddev, ColMeans or it could be user defined function.
Let’s take an example and use the function to see how it can help us.
ApplyFun = matrix(c(1:16), 4,4)
ApplyFun
apply(ApplyFun,2,sum)
apply(ApplyFun,2,mean)
apply(ApplyFun,1,var)
apply(ApplyFun,1,sum)
In the above code, we have applied sum and mean function on columns of the matrix; while variance and sum function on the rows. Let’s see the output of the above code.
> ApplyFun = matrix(c(1:16), 4,4)
> ApplyFun
[,1] [,2] [,3] [,4]
[1,] 1 5 9 13
[2,] 2 6 10 14
[3,] 3 7 11 15
[4,] 4 8 12 16
> apply(ApplyFun,2,sum)
[1] 10 26 42 58
> apply(ApplyFun,2,mean)
[1] 2.5 6.5 10.5 14.5
> apply(ApplyFun,1,var)
[1] 26.66667 26.66667 26.66667 26.66667
> apply(ApplyFun,1,sum)
[1] 28 32 36 40
Let’s understand the first statement that we executed; others are based on the same logic. We first generated a matrix as below:
> ApplyFun
[,1] [,2] [,3] [,4]
[1,] 1 5 9 13
[2,] 2 6 10 14
[3,] 3 7 11 15
[4,] 4 8 12 16
Now, in the second line [apply(ApplyFun,2,sum)], we are trying to calculate the sum of all the columns of the matrix. Here, ‘2’ means that the operation should be performed on the columns and sum is the function that should be executed. The output generated here is a vector.
Lapply Function
Lapply function is similar to apply function but it takes list or data frame as an input and returns list as an output. It has a similar syntax to apply function. Let’s take a couple of examples and see how it can be used.
LapplyFun = list(a = 1:5, b = 10:15, c = 21:25)
LapplyFun
lapply(LapplyFun, FUN = mean)
lapply(LapplyFun, FUN = median)
> LapplyFun = list(a = 1:5, b = 10:15, c = 21:25)
> LapplyFun
$a
[1] 1 2 3 4 5
$b
[1] 10 11 12 13 14 15
$c
[1] 21 22 23 24 25
> lapply(LapplyFun, FUN = mean)
$a
[1] 3
$b
[1] 12.5
$c
[1] 23
> lapply(LapplyFun, FUN = median)
$a
[1] 3
$b
[1] 12.5
$c
[1] 23
Sapply Function
Sapply function is similar to lapply, but it returns a vector as an output instead of list.
set.seed(5)
SapplyFun = list(a = rnorm(5), b = rnorm(5), c = rnorm(5))
SapplyFun
sapply(SapplyFun, FUN = mean)
> set.seed(5)
>
> SapplyFun = list(a = rnorm(5), b = rnorm(5), c = rnorm(5))
>
> SapplyFun
$a
[1] -0.84085548 1.38435934 -1.25549186 0.07014277 1.71144087
$b
[1] -0.6029080 -0.4721664 -0.6353713 -0.2857736 0.1381082
$c
[1] 1.2276303 -0.8017795 -1.0803926 -0.1575344 -1.0717600
>
> sapply(SapplyFun, FUN = mean)
a b c
0.2139191 -0.3716222 -0.3767672
Let’s take another example and see the difference between lapply and sapply in further detail.
X = matrix(1:9,3,3)
X
Y = matrix(11:19,3,3)
Y
Z = matrix(21:29,3,3)
Z
Comp.lapply.sapply = list(X,Y,Z)
Comp.lapply.sapply
> X = matrix(1:9,3,3)
> X
[,1] [,2] [,3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
>
> Y = matrix(11:19,3,3)
> Y
[,1] [,2] [,3]
[1,] 11 14 17
[2,] 12 15 18
[3,] 13 16 19
>
> Z = matrix(21:29,3,3)
> Z
[,1] [,2] [,3]
[1,] 21 24 27
[2,] 22 25 28
[3,] 23 26 29
> Comp.lapply.sapply = list(X,Y,Z)
> Comp.lapply.sapply
[[1]]
[,1] [,2] [,3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
[[2]]
[,1] [,2] [,3]
[1,] 11 14 17
[2,] 12 15 18
[3,] 13 16 19
[[3]]
[,1] [,2] [,3]
[1,] 21 24 27
[2,] 22 25 28
[3,] 23 26 29
lapply(Comp.lapply.sapply,"[", , 2)
lapply(Comp.lapply.sapply,"[", 1, )
lapply(Comp.lapply.sapply,"[", 1, 2)
> lapply(Comp.lapply.sapply,"[", , 2)
[[1]]
[1] 4 5 6
[[2]]
[1] 14 15 16
[[3]]
[1] 24 25 26
> lapply(Comp.lapply.sapply,"[", 1, )
[[1]]
[1] 1 4 7
[[2]]
[1] 11 14 17
[[3]]
[1] 21 24 27
> lapply(Comp.lapply.sapply,"[", 1, 2)
[[1]]
[1] 4
[[2]]
[1] 14
[[3]]
[1] 24
Now, getting the output of last statement using sapply function.
> sapply(Comp.lapply.sapply,"[", 1,2)
[1] 4 14 24
We can see the difference between lapply and sapply in the above example. Lapply returns the list as an output; while sapply returns vector as an output.
Mapply Function
Mapply function is similar to sapply function, which returns vector as an output and takes list as an input. Let’s take an example and understand how it works.
X = matrix(1:9,3,3)
X
Y = matrix(11:19,3,3)
Y
Z = matrix(21:29,3,3)
Z
mapply(sum,X,Y,Z)
> X = matrix(1:9,3,3)
> X
[,1] [,2] [,3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
>
> Y = matrix(11:19,3,3)
> Y
[,1] [,2] [,3]
[1,] 11 14 17
[2,] 12 15 18
[3,] 13 16 19
>
> Z = matrix(21:29,3,3)
> Z
[,1] [,2] [,3]
[1,] 21 24 27
[2,] 22 25 28
[3,] 23 26 29
>
> mapply(sum,X,Y,Z)
[1] 33 36 39 42 45 48 51 54 57
The above function adds element by element of each of the matrix and returns a vector as an output.
For e.g., 33 = X[1,1] + Y[1,1] + Z[1,1]
36 = X[2,1] + Y[2,1] + Z[2,1} and so on.
How to decide which apply function to use
Now, comes the part of deciding which apply function should one use and how to decide which apply function will provide the desired results. This is mainly based on the following four parameters:
- Input
-
Output
-
Intention
-
Section of Data
As we have discussed in the article above, all the apply family functions work on different types of datasets. Apply function works on arrays or matrices, lapply works on lists, sapply also works on lists and similar other functions. Based on kind of input that we are providing to the function provides us a first level of filter as to which all functions can be used.
Second filter comes from the output that we desire from the function. Lapply and sapply both work on lists; in that case, how to decide which function to use? As we saw above, lapply gives us list as an output while sapply outputs vector. This provides us another level of filter in deciding which function to choose.
Now, comes the intention which is making us use the apply family function. By intention, we mean the kind of functions that we are planning to pass through the apply family. Section of data refers to the subset or part of the data that we want our function to operate on – is it rows or columns or the entire dataset.
These four things can help us figure out which apply function should we choose for our tasks.
After going through the article, I’m sure you will agree with me that these functions are much easier to use than loops, and provides faster and efficient ways to execute codes. However, this doesn’t mean that we should not use loops at all. Loops have their own advantage when doing complex operations. Moreover, other programming languages do not provide any support for apply family function, so we don’t have an option but to use loops. We should keep ourselves open to both the ideas and decide what to use basis the requirements at hand.
Author Bio:
This article was contributed by
Perceptive Analytics. Chaitanya Sagar, Jyothirmayee Thondamallu and Saneesh Veetil contributed to this article.
Perceptive Analytics provides data analytics, data visualization, business intelligence and reporting services to e-commerce, retail, healthcare and pharmaceutical industries. Our client roster includes Fortune 500 and NYSE listed companies in the USA and India.
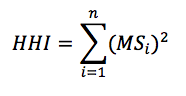 where MS is the market share of each firm, i, operating in a single market. Summing across all squared market shares for all firms results in the measure of concentration in the given market, HHI.
where MS is the market share of each firm, i, operating in a single market. Summing across all squared market shares for all firms results in the measure of concentration in the given market, HHI. 
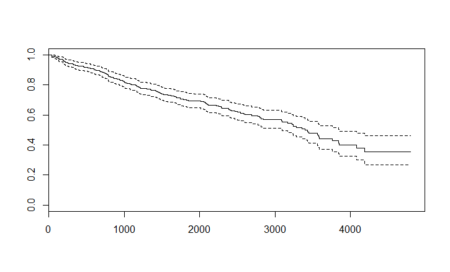
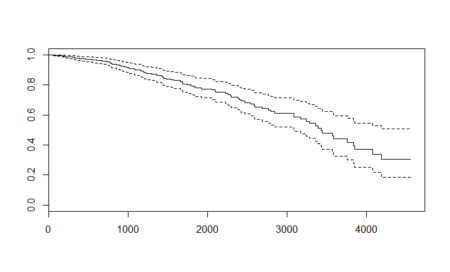
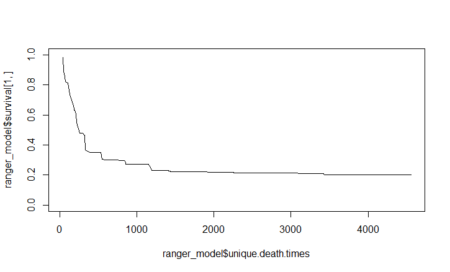
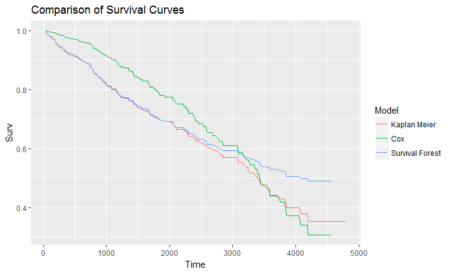


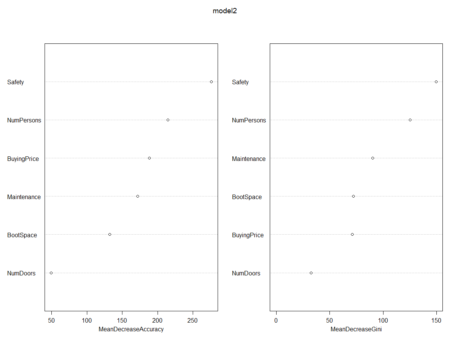
 In this post, taken from the book
In this post, taken from the book  My plan was the following—get the information from these cards and analyze it to discover whether some kind of common traits emerge.
My plan was the following—get the information from these cards and analyze it to discover whether some kind of common traits emerge.
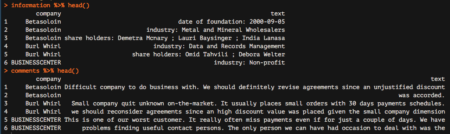 Great! We are nearly done. We are now going to start analyzing the comments data frame, which reports all comments from our colleagues. The very last step needed to make this data frame ready for subsequent analyzes is to tokenize it, which basically means separating it into different rows for all the words available within the text column. To do this, we are going to leverage the unnest_tokens function, which basically splits each line into words and produces a new row for each word, having taken care to repeat the corresponding value within the other columns of the original data frame.
This function comes from the recent tidytext package by Julia Silge and Davide Robinson, which provides an organic framework of utilities for text mining tasks. It follows the tidyverse framework, which you should already know about if you are using the dplyr package.
Let’s see how to apply the unnest_tokens function to our data:
Great! We are nearly done. We are now going to start analyzing the comments data frame, which reports all comments from our colleagues. The very last step needed to make this data frame ready for subsequent analyzes is to tokenize it, which basically means separating it into different rows for all the words available within the text column. To do this, we are going to leverage the unnest_tokens function, which basically splits each line into words and produces a new row for each word, having taken care to repeat the corresponding value within the other columns of the original data frame.
This function comes from the recent tidytext package by Julia Silge and Davide Robinson, which provides an organic framework of utilities for text mining tasks. It follows the tidyverse framework, which you should already know about if you are using the dplyr package.
Let’s see how to apply the unnest_tokens function to our data:
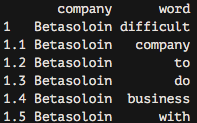 As you can see, we now have each word separated into a single record.
As you can see, we now have each word separated into a single record.