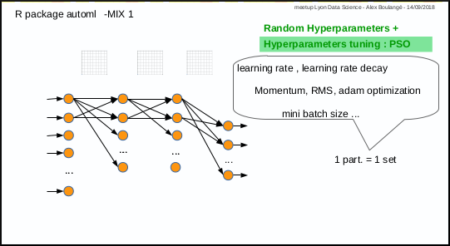
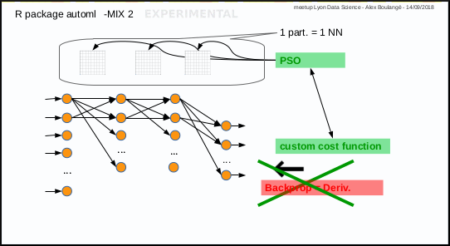
first steps: how to
For those who will laugh at seeing deep learning with one hidden layer and the Iris data set of 150 records, I will say: you’re perfectly right 🙂
The goal at this stage is simply to take the first steps
fit a regression model manually (hard way)
Subject: predict Sepal.Length given other Iris parameters
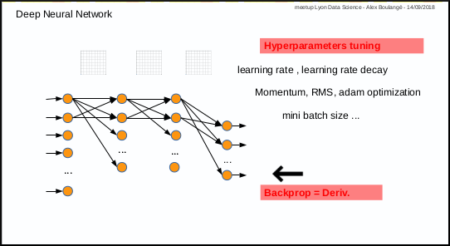
1st with gradient descent and default hyper-parameters value for learning rate (0.001) and mini batch size (32)
input
data(iris)
xmat <- cbind(iris[,2:4], as.numeric(iris$Species))
ymat <- iris[,1]
amlmodel <- automl_train_manual(Xref = xmat, Yref = ymat)
output
(cost: mse)
cost epoch10: 20.9340400047156 (cv cost: 25.205632342013) (LR: 0.001 )
cost epoch20: 20.6280923387762 (cv cost: 23.8214521197268) (LR: 0.001 )
cost epoch30: 20.3222407903838 (cv cost: 22.1899741289456) (LR: 0.001 )
cost epoch40: 20.0217966054298 (cv cost: 21.3908446693146) (LR: 0.001 )
cost epoch50: 19.7584058034009 (cv cost: 20.7170232035934) (LR: 0.001 )
dim X: ...
input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c('actual', 'predict')
head(res)
output
actual predict
[1,] 5.1 -2.063614
[2,] 4.9 -2.487673
[3,] 4.7 -2.471912
[4,] 4.6 -2.281035
[5,] 5.0 -1.956937
[6,] 5.4 -1.729314
:-[] no pain, no gain ...
After some manual fine tuning on learning rate, mini batch size and iterations number (epochs):
input
data(iris)
xmat <- cbind(iris[,2:4], as.numeric(iris$Species))
ymat <- iris[,1]
amlmodel = automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
learningrate = 0.01,
minibatchsize = 2^2,
numiterations = 30
)
)
output
(cost: mse)
cost epoch10: 5.55679482839698 (cv cost: 4.87492997304325) (LR: 0.01 )
cost epoch20: 1.64996951479802 (cv cost: 1.50339773126712) (LR: 0.01 )
cost epoch30: 0.647727077375946 (cv cost: 0.60142564484723) (LR: 0.01 )
dim X: ...
input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c('actual', 'predict')
head(res)
output
actual predict
[1,] 5.1 4.478478
[2,] 4.9 4.215683
[3,] 4.7 4.275902
[4,] 4.6 4.313141
[5,] 5.0 4.531038
[6,] 5.4 4.742847
Better result, but with human efforts!
fit a regression model automatically (easy way, Mix 1)
Same subject: predict Sepal.Length given other Iris parameters
input
data(iris)
xmat <- as.matrix(cbind(iris[,2:4], as.numeric(iris$Species)))
ymat <- iris[,1]
start.time <- Sys.time()
amlmodel <- automl_train(
Xref = xmat, Yref = ymat,
autopar = list(
psopartpopsize = 15,
numiterations = 5,
nbcores = 4
)
)
end.time <- Sys.time()
cat(paste('time ellapsed:', end.time - start.time, '\n'))
output
(cost: mse)
iteration 1 particle 1 weighted err: 22.05305 (train: 19.95908 cvalid: 14.72417 ) BEST MODEL KEPT
iteration 1 particle 2 weighted err: 31.69094 (train: 20.55559 cvalid: 27.51518 )
iteration 1 particle 3 weighted err: 22.08092 (train: 20.52354 cvalid: 16.63009 )
iteration 1 particle 4 weighted err: 20.02091 (train: 19.18378 cvalid: 17.09095 ) BEST MODEL KEPT
iteration 1 particle 5 weighted err: 28.36339 (train: 20.6763 cvalid: 25.48073 )
iteration 1 particle 6 weighted err: 28.92088 (train: 20.92546 cvalid: 25.9226 )
iteration 1 particle 7 weighted err: 21.67837 (train: 20.73866 cvalid: 18.38941 )
iteration 1 particle 8 weighted err: 29.80416 (train: 16.09191 cvalid: 24.66206 )
iteration 1 particle 9 weighted err: 22.93199 (train: 20.5561 cvalid: 14.61638 )
iteration 1 particle 10 weighted err: 21.18474 (train: 19.64622 cvalid: 15.79992 )
iteration 1 particle 11 weighted err: 23.32084 (train: 20.78257 cvalid: 14.43688 )
iteration 1 particle 12 weighted err: 22.27164 (train: 20.81055 cvalid: 17.15783 )
iteration 1 particle 13 weighted err: 2.23479 (train: 1.95683 cvalid: 1.26193 ) BEST MODEL KEPT
iteration 1 particle 14 weighted err: 23.1183 (train: 20.79754 cvalid: 14.99564 )
iteration 1 particle 15 weighted err: 20.71678 (train: 19.40506 cvalid: 16.12575 )
...
iteration 4 particle 3 weighted err: 0.3469 (train: 0.32236 cvalid: 0.26104 )
iteration 4 particle 4 weighted err: 0.2448 (train: 0.07047 cvalid: 0.17943 )
iteration 4 particle 5 weighted err: 0.09674 (train: 5e-05 cvalid: 0.06048 ) BEST MODEL KEPT
iteration 4 particle 6 weighted err: 0.71267 (train: 6e-05 cvalid: 0.44544 )
iteration 4 particle 7 weighted err: 0.65614 (train: 0.63381 cvalid: 0.57796 )
iteration 4 particle 8 weighted err: 0.46477 (train: 0.356 cvalid: 0.08408 )
...
time ellapsed: 2.65109273195267
input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c('actual', 'predict')
head(res)
output
actual predict
[1,] 5.1 5.193862
[2,] 4.9 4.836507
[3,] 4.7 4.899531
[4,] 4.6 4.987896
[5,] 5.0 5.265334
[6,] 5.4 5.683173
It's even better, with no human efforts but machine time
Users on Windows won't benefit from parallelization, the function uses parallel package included with R base...
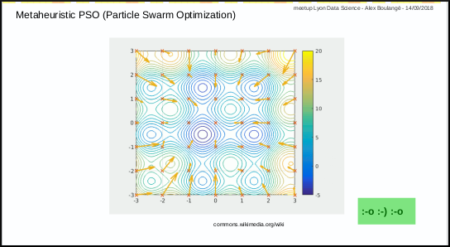
fit a regression model experimentally (experimental way, Mix 2)
Same subject: predict Sepal.Length given other Iris parameters
input
data(iris)
xmat <- as.matrix(cbind(iris[,2:4], as.numeric(iris$Species)))
ymat <- iris[,1]
amlmodel <- automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
modexec = 'trainwpso',
numiterations = 30,
psopartpopsize = 50
)
)
output
(cost: mse)
cost epoch10: 0.113576786377019 (cv cost: 0.0967069106128153) (LR: 0 )
cost epoch20: 0.0595472259640828 (cv cost: 0.0831404427407914) (LR: 0 )
cost epoch30: 0.0494578776185938 (cv cost: 0.0538888075333611) (LR: 0 )
dim X: ...
input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c('actual', 'predict')
head(res)
output
actual predict
[1,] 5.1 5.028114
[2,] 4.9 4.673366
[3,] 4.7 4.738188
[4,] 4.6 4.821392
[5,] 5.0 5.099064
[6,] 5.4 5.277315
Pretty good too, even
better!
But time consuming on larger datasets: where gradient descent should be preferred in this case
fit a regression model with custom cost (experimental way, Mix 2)
Same subject: predict Sepal.Length given other Iris parameters
Let's try with Mean Absolute Percentage Error instead of Mean Square Error
input
data(iris)
xmat <- as.matrix(cbind(iris[,2:4], as.numeric(iris$Species)))
ymat <- iris[,1]
f <- 'J=abs((y-yhat)/y)'
f <- c(f, 'J=sum(J[!is.infinite(J)],na.rm=TRUE)')
f <- c(f, 'J=(J/length(y))')
f <- paste(f, collapse = ';')
amlmodel <- automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
modexec = 'trainwpso',
numiterations = 30,
psopartpopsize = 50,
costcustformul = f
)
)
output
(cost: custom)
cost epoch10: 0.901580275333795 (cv cost: 1.15936129555304) (LR: 0 )
cost epoch20: 0.890142834441629 (cv cost: 1.24167078564786) (LR: 0 )
cost epoch30: 0.886088388448652 (cv cost: 1.22756121243449) (LR: 0 )
dim X: ...
input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c('actual', 'predict')
head(res)
output
actual predict
[1,] 5.1 4.693915
[2,] 4.9 4.470968
[3,] 4.7 4.482036
[4,] 4.6 4.593667
[5,] 5.0 4.738504
[6,] 5.4 4.914144
fit a classification model with softmax (Mix 2)
Subject: predict Species given other Iris parameters
Softmax is available with PSO, no derivative needed 😉
input
data(iris)
xmat = iris[,1:4]
lab2pred <- levels(iris$Species)
lghlab <- length(lab2pred)
iris$Species <- as.numeric(iris$Species)
ymat <- matrix(seq(from = 1, to = lghlab, by = 1), nrow(xmat), lghlab, byrow = TRUE)
ymat <- (ymat == as.numeric(iris$Species)) + 0
amlmodel <- automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
modexec = 'trainwpso',
layersshape = c(10, 0),
layersacttype = c('relu', 'softmax'),
layersdropoprob = c(0, 0),
numiterations = 50,
psopartpopsize = 50
)
)
output
(cost: crossentropy)
cost epoch10: 0.373706545886467 (cv cost: 0.36117608867856) (LR: 0 )
cost epoch20: 0.267034060152876 (cv cost: 0.163635821437066) (LR: 0 )
cost epoch30: 0.212054571476337 (cv cost: 0.112664100290429) (LR: 0 )
cost epoch40: 0.154158717402463 (cv cost: 0.102895917099299) (LR: 0 )
cost epoch50: 0.141037927317585 (cv cost: 0.0864623836595045) (LR: 0 )
dim X: ...
input
res <- cbind(ymat, automl_predict(model = amlmodel, X = xmat))
colnames(res) <- c(paste('act',lab2pred, sep = '_'),
paste('pred',lab2pred, sep = '_'))
head(res)
tail(res)
output
act_setosa act_versicolor act_virginica pred_setosa pred_versicolor pred_virginica
1 1 0 0 0.9863481 0.003268881 0.010383018
2 1 0 0 0.9897295 0.003387193 0.006883349
3 1 0 0 0.9856347 0.002025946 0.012339349
4 1 0 0 0.9819881 0.004638452 0.013373451
5 1 0 0 0.9827623 0.003115452 0.014122277
6 1 0 0 0.9329747 0.031624836 0.035400439
act_setosa act_versicolor act_virginica pred_setosa pred_versicolor pred_virginica
145 0 0 1 0.02549091 2.877957e-05 0.9744803
146 0 0 1 0.08146753 2.005664e-03 0.9165268
147 0 0 1 0.05465750 1.979652e-02 0.9255460
148 0 0 1 0.06040415 1.974869e-02 0.9198472
149 0 0 1 0.02318048 4.133826e-04 0.9764061
150 0 0 1 0.03696852 5.230936e-02 0.9107221
change the model parameters (shape ...)
Same subject: predict Species given other Iris parameters
1st example: with gradient descent and 2 hidden layers containing 10 nodes, with various activation functions for hidden layers
input
data(iris)
xmat = iris[,1:4]
lab2pred <- levels(iris$Species)
lghlab <- length(lab2pred)
iris$Species <- as.numeric(iris$Species)
ymat <- matrix(seq(from = 1, to = lghlab, by = 1), nrow(xmat), lghlab, byrow = TRUE)
ymat <- (ymat == as.numeric(iris$Species)) + 0
amlmodel <- automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
layersshape = c(10, 10, 0),
layersacttype = c('tanh', 'relu', ''),
layersdropoprob = c(0, 0, 0)
)
)
nb: last activation type may be left to blank (it will be set automatically)
2nd example: with gradient descent and no hidden layer (logistic regression)
input
data(iris)
xmat = iris[,1:4]
lab2pred <- levels(iris$Species)
lghlab <- length(lab2pred)
iris$Species <- as.numeric(iris$Species)
ymat <- matrix(seq(from = 1, to = lghlab, by = 1), nrow(xmat), lghlab, byrow = TRUE)
ymat <- (ymat == as.numeric(iris$Species)) + 0
amlmodel <- automl_train_manual(
Xref = xmat, Yref = ymat,
hpar = list(
layersshape = c(0),
layersacttype = c('sigmoid'),
layersdropoprob = c(0)
)
)
ToDo List
- transfert learning from existing frameworks
- add autotune to other parameters (layers, dropout, ...)
- CNN
- RNN
join the team !
https://github.com/aboulaboul/automl