In this article, we discuss the basics of ordinal logistic regression and its implementation in R. Ordinal logistic regression is a widely used classification method, with applications in variety of domains. This method is the go-to tool when there is a natural ordering in the dependent variable. For example, dependent variable with levels low, medium, high is a perfect context for application of logistic ordinal regression.
Having wide range of applicability, ordinal logistic regression is considered as one of the most admired methods in the field of data analytics. The method is also known as proportional odds model because of the transformations used during estimation and the log odds interpretation of the output. We hope that this article helps our readers to understand the basics and implement the model in R. The article is organized as follows: focusing on the theoretical aspects of the technique, section 1 provides a quick review of ordinal logistic regression. Section 2 discusses the steps to perform ordinal logistic regression in R and shares R script. In addition, section 2 also covers the basics of interpretation and evaluation of the model on R. In section 3, we learn a more intuitive way to interpret the model. Section 4 concludes the article.
Basics of ordinal logistic regression
Ordinal logistic regression is an extension of simple logistic regression model. In simple logistic regression, the dependent variable is categorical and follows a Bernoulli distribution. (for a quick reference check out this article by perceptive analytics – https://www.kdnuggets.com/2017/10/learn-generalized-linear-models-glm-r.html). Whereas, in ordinal logistic regression the dependent variable is ordinal i.e. there is an explicit ordering in the categories. For example, during preliminary testing of a pain relief drug, the participants are asked to express the amount of relief they feel on a five point Likert scale. Another common example of an ordinal variable is app ratings. On google play, customers are asked to rate apps on a scale ranging from 1 to 5. Ordinal logistic regression becomes handy in the aforementioned examples as there is a clear order in the categorical dependent variable.
In simple logistic regression, log of odds that an event occurs is modeled as a linear combination of the independent variables. But, the above approach of modeling ignores the ordering of the categorical dependent variable. Ordinal logistic regression model overcomes this limitation by using cumulative events for the log of the odds computation. It means that unlike simple logistic regression, ordinal logistic models consider the probability of an event and all the events that are below the focal event in the ordered hierarchy. For example, the event of interest in ordinal logistic regression would be to obtain an app rating equal to X or less than X. For example, the log of odds for the app rating less than or equal to 1 would be computed as follows:
LogOdds rating<1 = Log (p(rating=1)/p(rating>1) [Eq. 1]
Likewise, the log of odds can be computed for other values of app ratings. The computations for other ratings are below: LogOdds rating<2 = Log (p(rating<=2)/p(rating>2) [Eq. 2] LogOdds rating<3 = Log (p(rating<=3)/p(rating>3) [Eq. 3] LogOdds rating<4 = Log (p(rating=4)/p(rating>4) [Eq. 4]
Because all the ratings below the focal score are considered in computation, the highest app rating of 5 will include all the ratings below it and does not have a log of odds associated with it. In general, the ordinal regression model can be represented using the LogOdds computation.
LogoddsY = αi+ β1X1 +β2X2 +….. +βnXn
where,
Y is the ordinal dependent variable
i is the number of categories minus 1
X1, X2,…. Xn are independent variables. They can be measured on nominal, ordinal or continuous measurement scale.
β1, β2,… βn are estimated parameters For i ordered categories, we obtain i – 1 equations. The proportional odds assumption implies that the effect of independent variables is identical for each log of odds computation. But, this is not the case for intercept as the intercept takes different values for each computation. Besides the proportional odds assumption, the ordinal logistic regression model assumes an ordinal dependent variable and absence of multicollinearity. Absence of multicollinearity means that the independent variables are not significantly correlated. These assumptions are important as their violation makes the computed parameters unacceptable.
Model building in R In this section, we describe the dataset and implement ordinal logistic regression in R. We use a simulated dataset for analysis. The details of the variables are as follows. The objective of the analysis is to predict the likelihood of each level of customer purchase. The dependent variable is the likelihood of repeated purchase by customers. The variable is measured in an ordinal scale and can be equal to one of the three levels – low probability, medium probability, and high probability. The independent variables are measures of possession of coupon by the focal customer, recommendation received by the peers and quality of the product. Possession of coupon and peer recommendation are categorical variables, while quality is measured on a scale of 1 to 5. We discuss the steps for implementation of ordinal logistic regression and share the commented R script for better understanding of the reader. The data is in .csv format and can be downloaded by clicking here. Before starting the analysis, I will describe the preliminary steps in short. The first step is to keep the data file in the working directory. The next step is to explicitly define the ordering of the levels in the dependent variable and the relevant independent variables. This step is crucial and ignoring it can lead to meaningless analysis.
#Read data file from working directory
setwd("C:/Users/You/Desktop")
data <- read.table("data.txt")
#Ordering the dependent variable
data$rpurchase = factor(data$rpurchase, levels = c("low probability", "medium probability", "high probability"), ordered = TRUE)
data$peers = factor(data$peers, levels = c("0", "1"), ordered = TRUE)
data$coupon = factor(data$coupon, levels = c("0", "1"), ordered = TRUE)
Next, it is essential to perform the exploratory data analysis. Exploratory data analysis deals with outliers and missing values, which can induce bias in our model. In this article we do basic exploration by looking at summary statistics and frequency table. Figure 1. shows the summary statistics. We observe the count of data for ordinal variables and distribution characteristics for other variables. We compute the count of rpurchase with different values of coupon in Table 1. Note that the median value for rpurchase changes with change in coupon. The median level of rpurchase increases, indicating that coupon positively affects the likelihood of repeated purchase. The R script for summary statistics and the frequency table is as follows:#Exploratory data analysis
#Summarizing the data
summary(data)
#Making frequency table
table(data$rpurchase, data$coupon)
Figure 1. Summary statistics
| Rpurchase/Coupon | With coupon | Without coupon |
| Low probability | 200 | 20 |
| Medium probability | 110 | 30 |
| High proabability | 27 | 13 |
#Dividing data into training and test set #Random sampling samplesize = 0.60*nrow(data) set.seed(100) index = sample(seq_len(nrow(data)), size = samplesize) #Creating training and test set datatrain = data[index,] datatest = data[-index,]Now, we will build the model using the data in training set. As discussed in the above section the dependent variable in the model is in the form of log odds. Because of the log odds transformation, it is difficult to interpret the coefficients of the model. Note that in this case the coefficients of the regression cannot be interpreted in terms of marginal effects. The coefficients are called as proportional odds and interpreted in terms of increase in log odds. The interpretation changes not only for the coefficients but also for the intercept. Unlike simple linear regression, in ordinal logistic regression we obtain n-1 intercepts, where n is the number of categories in the dependent variable. The intercept can be interpreted as the expected odds of identifying in the listed categories. Before interpreting the model, we share the relevant R script and the results. In the R code, we set Hess equal to true which the logical operator to return hessian matrix. Returning the hessian matrix is essential to use summary function or calculate variance-covariance matrix of the fitted model.
#Build ordinal logistic regression model model= polr(rpurchase ~ coupon + peers + quality , data = datatrain, Hess = TRUE) summary(model)Figure 2. Ordinal logistic regression model on training set
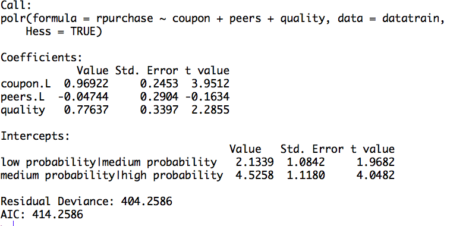
The table displays the value of coefficients and intercepts, and corresponding standard errors and t values. The interpretation for the coefficients is as follows. For example, holding everything else constant, an increase in value of coupon by one unit increase the expected value of rpurchase in log odds by 0.96. Likewise, the coefficients of peers and quality can be interpreted.
Note that the ordinal logistic regression outputs multiple values of intercepts depending on the levels of intercept. The intercepts can be interpreted as the expected odds when others variables assume a value of zero. For example, the low probability | medium probability intercept takes value of 2.13, indicating that the expected odds of identifying in low probability category, when other variables assume a value of zero, is 2.13. Using the logit inverse transformation, the intercepts can be interpreted in terms of expected probabilities. The inverse logit transformation, <to be inserted> . The expected probability of identifying low probability category, when other variables assume a value of zero, is 0.89. After building the model and interpreting the model, the next step is to evaluate it. The evaluation of the model is conducted on the test dataset. A basic evaluation approach is to compute the confusion matrix and the misclassification error. The R code and the results are as follows:
#Compute confusion table and misclassification error predictrpurchase = predict(model,datatest) table(datatest$rpurchase, predictrpurchase) mean(as.character(datatest$rpurchase) != as.character(predictrpurchase))Figure 3. Confusion matrix
Interpretation using plots
The interpretation of the logistic ordinal regression in terms of log odds ratio is not easy to understand. We offer an alternative approach to interpretation using plots. The R code for plotting the effects of the independent variables is as follows:
#Plotting the effects
library("effects")
Effect(focal.predictors = "quality",model)
plot(Effect(focal.predictors = "coupon",model))
plot(Effect(focal.predictors = c("quality", "coupon"),model))
The plots are intuitive and easy to understand. For example, figure 4 shows that coupon increases the likelihood of classification into high probability and medium probability classes, while decreasing the likelihood of classification in low probability class.Figure 4. Effect of coupon on identification
It is also possible to look at joint effect of two independent variable. Figure 5. shows the joint effect of quality and coupon on identification of category of independent variable. Observing the top row of figure 5., we notice that the interaction of coupon and quality increases the likelihood of identification in high probability category.
Figure 5. Joint effect of quality and coupon on identification
Conclusion The article discusses the fundamentals of ordinal logistic regression, builds and the model in R, and ends with interpretation and evaluation. Ordinal logistic regression extends the simple logistic regression model to the situations where the dependent variable is ordinal, i.e. can be ordered. Ordinal logistic regression has variety of applications, for example, it is often used in marketing to increase customer life time value. For example, consumers can be categorized into different classes based on their tendency to make repeated purchase decision. In order to discuss the model in an applied manner, we develop this article around the case of consumer categorization. The independent variables of interest are – coupon held by consumers from previous purchase, influence of peers, quality of the product. The article has two key takeaways. First, ordinal logistic regression come handy while dealing with a dependent variable that can be ordered. If one uses multinomial logistic regression then the user is ignoring the information related to ordering of the dependent variable. Second, the coefficients of the ordinal linear regression cannot be interpreted in a similar manner to the coefficients of ordinary linear regression. Interpreting the coefficents in terms of marginal effects is one of the common mistakes that users make while implementing the ordinal regression model. We again emphasize the use of graphical method to interpret the coefficients. Using the graphical method, it is easy to understand the individual and joint effects of independent variables on the likelihood of classification. This article can be a go to reference for understanding the basics of ordinal logistic regression and its implementation in R. We have provided commented R code throughout the article.
Download R-code
Credits: Chaitanya Sagar and Aman Asija of Perceptive Analytics. Perceptive Analytics is a marketing analytics and Tableau consulting company.