In practice, survival times may be influenced by a combination of baseline variables. Survival trees (i.e., trees with survival data) offer a relatively flexible approach to understanding the effects of covariates, including their interaction, on survival times when the functional form of the association is unknown, and also have the advantage of easier interpretation. This blog presents the construction of a survival tree following the SurvCART algorithm (Kundu and Ghosh 2021). Usually, a survival tree is constructed based on the heterogeneity in time-to-event distribution. However, in some applications with marker dependent censoring (e.g., less education or better prognosis might lead to early censoring) ignorance of censoring distribution might lead to inconsistent survival tree (Cui, Zhou and Kosorok, 2021). Therefore, the SurvCART algorithm is flexible to construct a survival tree based on heterogeneity both in time-to-event and censoring distribution. However, it is important to emphasize that the use of censoring heterogeneity in the construction of survival trees is optional. In this blog, the construction of a survival tree is illustrated with an R dataset in step by step approach and the results are explained using the functions available in the LongCART package.
Installing and Loading LongCART package
R> install.packages("LongCART")
R> library(LongCART)
The GBSG2 datasetWe will illustrate the SurvCART algorithm with GBSG2 data to analyze recurrence-free survival (RFS) originated from a prospective randomized clinical trial conducted by the German Breast Cancer Study Group. The purpose is to evaluate the effect of prognostic factors on RFS among node-positive breast cancer patients receiving chemotherapy in the adjuvant setting. RFS is time-to-event endpoint which was defined as the time from mastectomy to the first occurrence of either recurrence, contralateral or secondary tumor, or death. This GBSG2 dataset is included in the LongCART package in R. The dataset contains the information from 686 breast cancer patients with the following variables: time (RFS follow-up time in days), cens (censoring indicator: 0[censored], 1[event]), horTH (hormonal therapy: yes, no), age (age in years), menostat (menopausal status: pre, post), tsize (tumour size in mm), tgrade (tumour grade: I, II, III), pnodes (number of positive nodes), progrec (level of progesterone receptor[PR] in fmol), and estrec (level of the estrogen receptor in fmol). For details about the conduct of the study, please refer to Schumacher et al.
Let’s first explore the dataset.
R> library(speff2trial)
R> data("ACTG175", package = "speff2trial")
R> adata<- reshape(data=ACTG175[,!(names(ACTG175) %in% c("cd80", "cd820"))],
+ varying=c("cd40", "cd420", "cd496"), v.names="cd4",
+ idvar="pidnum", direction="long", times=c(0, 20, 96))
R> adata<- adata[order(adata$pidnum, adata$time),]
The median RFS time based on the entire 686 patients was 60 months with a total of 299 reported RFS events. Does any baseline covariate influence the median RFS time and if yes then how? A survival tree is meant to find this answer. Impact of individual categorical baseline variables on RFS
We would like to start with understanding the impact of individual baseline covariates on the median RFS time. There could be two types of baseline covariates: categorical (e.g., horTH [hormonal therapy]) and continuous (e.g., age). The impact of an individual categorical variable can be statistically assessed using
StabCat.surv() [Note: StabCat.surv() performs a statistical test as described in Section 2.2.1 of Kundu and Ghosh 2021].Let’s focus only on the heterogeneity in RFS (assuming exponential underlying distribution for RFS), but not on the censoring distribution.
R> out1<- StabCat.surv(data=GBSG2, timevar="time", censorvar="cens", R> splitvar="horTh", time.dist="exponential", R> event.ind=1) Stability Test for Categorical grouping variable Test.statistic= 8.562, Adj. p-value= 0.003 Greater evidence of heterogeneity in time-to-event distribution R> out1$pval [1] 0.003431809The p-value is 0.00343 suggesting the influence of hormonal therapy on RFS. Here we considered Exponential distribution for RFS, but the following distributions can be specified as well:
"weibull", "lognormal" or "normal". Now we illustrate the use of
StabCat.surv() considering heterogeneity both in RFS time and censoring time.R> out1<- StabCat.surv(data=GBSG2, timevar="time", censorvar="cens", R> splitvar="horTh", time.dist="exponential", R> cens.dist="exponential", event.ind=1) Stability Test for Categorical grouping variable Test.statistic= 8.562 0.013, Adj. p-value= 0.007 0.909 Greater evidence of heterogeneity in time-to-event distribution > out1$pval [1] 0.006863617Note the two
Test.statistic values (8.562 and 0.013): the first one corresponds to for heterogeneity in RFS time and the second one corresponds to heterogeneity in censoring distribution. Consequently, we also see the two p-values (adjusted). The overall p-value 0.006863617. In comparison to the earlier p-value of 0.00343, this p-value is greater due to the multiplicity adjustment.Impact of individual continuous baseline variables on RFS
Similarly, we can assess the impact of an individual continuous variable by performing a statistical test as described in Section 2.2.2 of Kundu and Ghosh 2021 which is implemented in
StabCont.surv()R> out1<- StabCont.surv(data=GBSG2, timevar="time", censorvar="cens", R> splitvar="age", time.dist="exponential", R> event.ind=1) Stability Test for Continuous grouping variable Test.statistic= 0.925, Adj. p-value= 0.359 Greater evidence of heterogeneity in time-to-event distribution > out1$pval [1] 0.3591482The p-value is 0.3591482 suggesting no impact of age on RFS. Heterogeneity in censoring distribution can be considered here as well by specifying
cens.dist as shown with StabCat.surv().Construction of survival tree
A survival tree can be constructed using
SurvCART(). Note that the SurvCART() function currently can handle the categorical baseline variables with numerical levels only. For nominal variables, please create the corresponding numerically coded dummy variable(s) as has been done below for horTh, trade and menostat
R> GBSG2$horTh1<- as.numeric(GBSG2$horTh)
R> GBSG2$tgrade1<- as.numeric(GBSG2$tgrade)
R> GBSG2$menostat1<- as.numeric(GBSG2$menostat)
We also have to add the subject id if that is not already there.R> GBSG2$subjid<- 1:nrow(GBSG2)
In the SurvCART(), we have to list out all the baseline variables of interest and declare whether it is categorical or continuous. Further, we also have to specify the RFS distribution "exponential"(default), "weibull", "lognormal" or "normal". The censoring distribution could be "NA"(default: i.e., no censoring heterogeneity), "exponential" "weibull", "lognormal" or "normal". Let’s construct the survival tree with heterogeneity in RFS only (i.e., ignoring censoring heterogeneity)
R> out.tree<- SurvCART(data=GBSG2, patid="subjid", R> censorvar="cens", timevar="time", R> gvars=c('horTh1', 'age', 'menostat1', 'tsize', R> 'tgrade1', 'pnodes', 'progrec', 'estrec'), R> tgvars=c(0,1,0,1,0,1, 1,1), R> time.dist="exponential", R> event.ind=1, alpha=0.05, minsplit=80, minbucket=40, R> print=TRUE)All the baseline variables are listed in gvars argument. The tgvars argument is accompanied with the gvars argument which indicates type of the partitioning variables (0=categorical or 1=continuous). Further, we have considered exponential distribution for RFS time.
Within
SurvCART(), at any given tree-node, each of the baseline variables is tested for heterogeneity using eitherStabCat.surv() or StabCont.surv() and the corresponding p-value is obtained. Further, these p-values are adjusted according to the Hochberg procedure and subsequently, the baseline variable with the smallest p-value is selected. These details would be printed if print=TRUE. This procedure keeps iterating until we hit the terminal node (i.e., no more statistically significant baseline variable, node size is smaller than the minsplit or further splitting results in a node size smaller than minbucket).Now let’s view the tree result
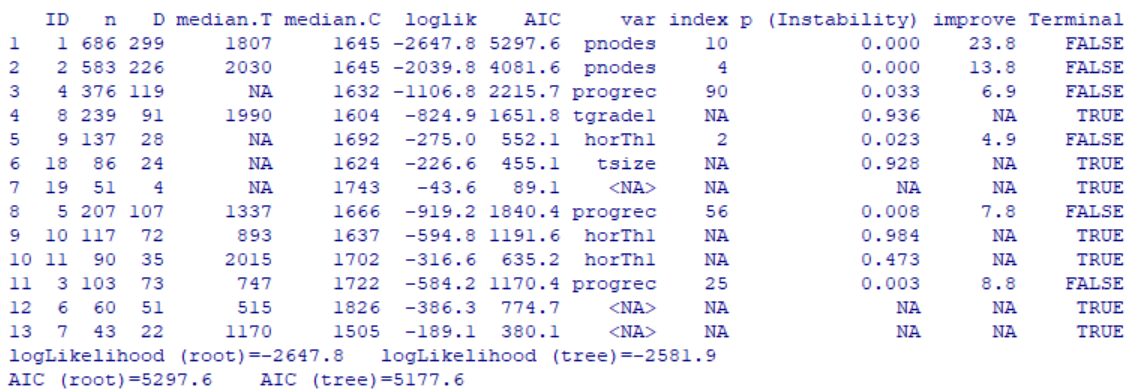
In the above output, each row corresponds to a single node including the 7 terminal nodes identified by TERMINAL=TRUE. Now let’s visualize the tree result
R> par(xpd = TRUE)
R> plot(out.tree, compress = TRUE)
R> text(out.tree, use.n = TRUE)
The resultant tree is as follows: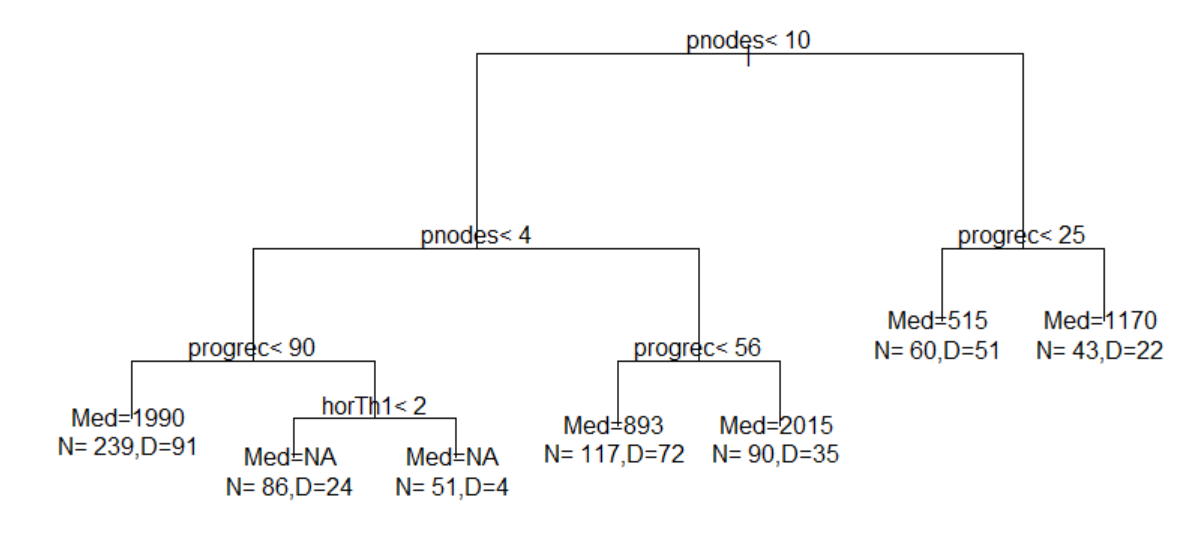
We can also plot KM plot for sub-groups identified by survival tree as follows:
KMPlot.SurvCART(out.tree, scale.time=365.25, type=1)
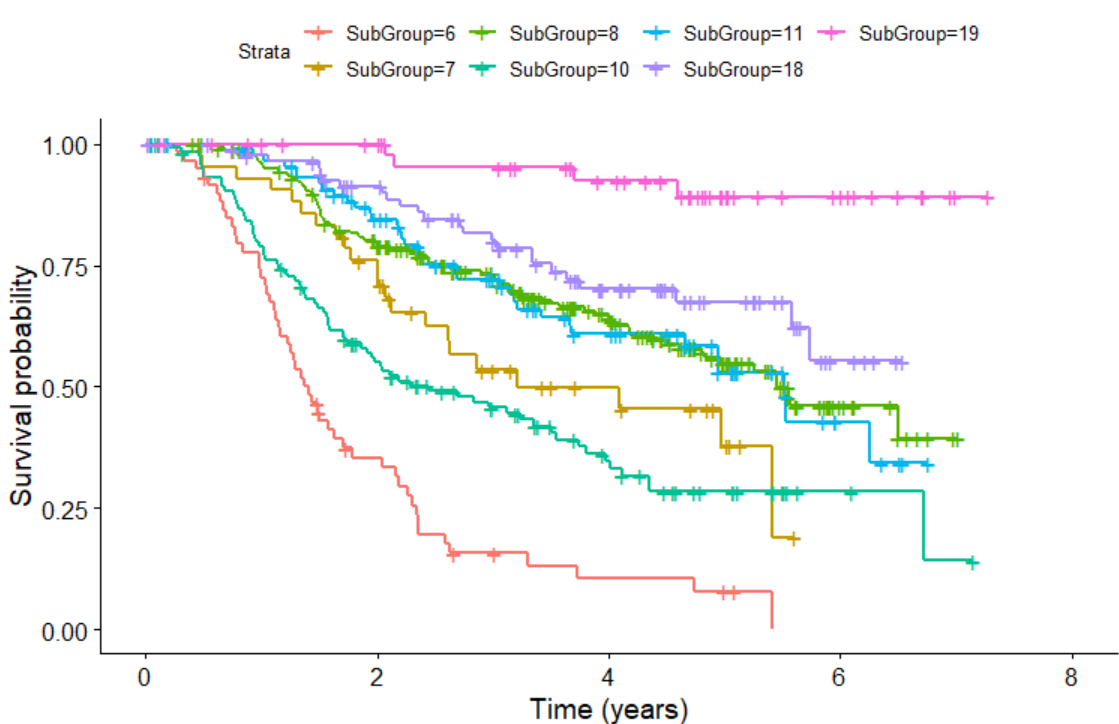
Last but not least, we can consider heterogeneity in censoring distribution in
SurvCART() by specifying cens.dist .Reference
1. Kundu, M. G., & Ghosh, S. (2021). Survival trees based on heterogeneity in time‐to‐event and censoring distributions using parameter instability test. Statistical Analysis and Data Mining: The ASA Data Science Journal, 14(5), 466-483. [link]
2. Y. Cui, R. Zhu, M. Zhou, and M. Kosorok, Consistency of survival tree and forest models: Splitting bias and correction. Statistica Sinica Preprint No: SS-2020-0263, 2021.
3. Schumacher, M., Bastert, G., Bojar, H., Hübner, K., Olschewski, M., Sauerbrei, W., … & Rauschecker, H. F. (1994). Randomized 2 x 2 trial evaluating hormonal treatment and the duration of chemotherapy in node-positive breast cancer patients. German Breast Cancer Study Group. Journal of Clinical Oncology, 12(10), 2086-2093. [link]
4. LongCART package v 3.1 or higher, https://CRAN.R-project.org/package=LongCART